Sin2x Formula

There are 2 Sin2x formula, i.e., Sin2x= 2sinx cosx and Sin2x= 2tan (x)/ 1 + tan 2x. Trigonometry is a fun but fundamental mathematical subject.In trigonometry, which is widely used in science, we investigate a number of formulas, theorems, and equations. 

Formula of Sin2x

The Sin2x formula is one of many double-angle formulas that can be found in trigonometry. We can use this formula to determine the sine of the angle whose value is doubled.

The ratio of the length of the opposite side to the length of the hypotenuse in a right-angled triangle is known as the sin function, which is one of the primary trigonometric ratios.

Basic trigonometric formulas can be used to derive numerous sin 2x-related formulas.

Formulas and identities of sin 2x, cos 2x, tan 2x, cot 2x, sec 2x and cosec 2x are known as double angle formulas because they have angles double of the angle present in their formulas.

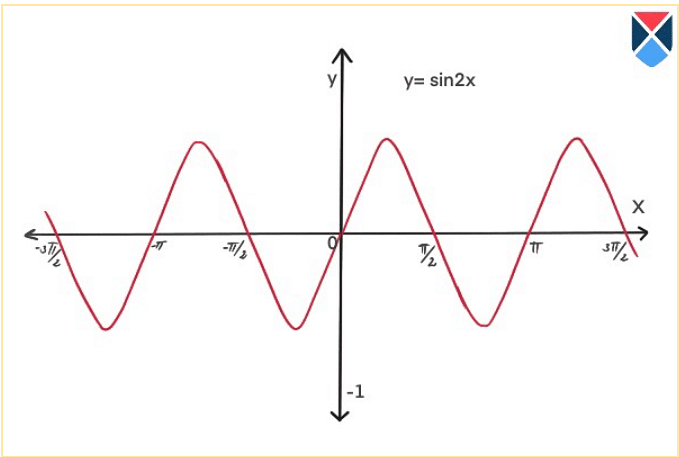
The graph above shows the relation between x and y axis where it is shown that y= Sin2x. 

How Formula Sin 2x Derived

First, to start with the known formula which is sin and cos are multiples of each other. 

This approach leads to a formula that is known as the angle sum formula of sin.

To derive the Sin2x formula, the angle sum formula of sin can be used. 

The sum formula of sin is sin(A + B) = sin A cos B + sin B cos A. 

Let us see the derivation of sin2x step by step:

Substitute A = B = x in the formula sin(A + B) = sin A cos B + sin B cos A,

sin(x + x) = sin x cos x + sin x cos x

⇒ sin2x = 2 sin x cos x

Hence, we have derived the formula of sin2x.

Sin 2x Formula in Terms of Tan

The Sin2x formula is explained in different ways, the given steps below will explain the Sin2x formula in terms of Tan

Sin2x = 2sinx cosx

Multiply and divide the above equation by cos x. Then

sin2x = (2 sin x cos2x)/(cos x) = 2 (sin x/cosx ) × (cos2x)

We know that sin x/cos x = tan x and cos x = 1/(sec x). 

So sin2x = 2 tan x × (1/sec2x)

Using one of the Pythagorean trigonometric identities, sec2x = 1 + tan2x. 

Substituting this, we have sin2x = (2tan x)​/(1 + tan2x)

Therefore, the sin2x formula in terms of tan is sin2x = (2tan x)​/(1 + tan2x).

Solved Question Samples Using Sin2x Formula

These double angle formulas, more specifically the cos2x and sin2x formula, are utilized in significant integration and differentiation problems. They are utilized in actual height and distance problems as well as in pure mathematics. 

The cos 2x and sin 2x double-angle formulas accomplish this simplification.

Question 1: Find the Value 2sinx sin2x Formula in Terms of Cos.

Answer: We can simplify the given expression by substituting the value of sin 2x. We know that  

Sin (2x) = 2Sin x Cos x 

On substituting the value we get,

2sin x sin2x =2sinx 2sinxcosx

2sinxsin2x =4sin2xcosx

Since we need to get this expression in cos we can use the identity Sin2θ + Cos2θ = 1. We get,

2sinxsin2x = 4(1-cos2x)cosx

2sinxsin2x = 4cosx-4cos3x

Question 2: Find value of sin90∘ using its double angle Sin2x  formula.

Answer:  Sin2x formula for double angle is 2Sinx Cosx

Putting  x=45∘

Sin(2×45∘)=2 Sin45∘ Cos45∘

Since  Sin45∘=1/√2

Cos45∘=1/√2

Therefore, by substituting the results will be:

Sin90∘=2×1/√2 ×1/√2

=2×1/2=1

Thus value of is Sin90∘1.

Important Notes on Sin2x

• The important formula of sin2x is sin2x = 2 sin x cos x and sin2x = (2tan x)​/(1 + tan2x)
• The formula for sin^2x is sin^2x = 1 - cos^2x and sin^2x = (1 - cos2x)/2
• Sin2x formula is called the double angle formula of the sine function.

History of Trigonometry

The Greek mathematician Hipparchus produced the first known table of chords in about 140 BC. Although these tables have not survived, it is claimed that Hipparchus wrote twelve books of tables of chords, making Hipparchus the founder of trigonometry.