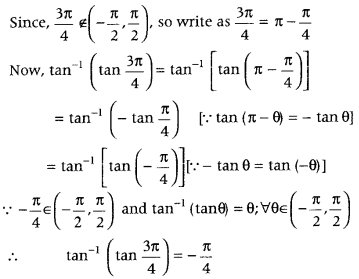CBSE 12th Maths Exam to Be Held on Mar 11: Check CBSE 12th Mathematics Chapter 2 Important Questions
Students can refer to the CBSE 12th Mathematics Chapter 2 Important Questions and solutions here to prepare for their upcoming CBSE Board Exam 2023.
CBSE 12th Mathematics Chapter 2 Important Questions: The Central Board of Secondary Education (CBSE), India, is all set to conduct the class 12 Board exams from Feb 15 to Apr 5, 2023.
The Mathematics exam is scheduled to be held on Mar 11. Students completing their CBSE 12th Mathematics revision must thoroughly study the 2nd chapter, i.e., CBSE 12th Mathematics Inverse Trigonometric Functions.
Continue reading further to check the CBSE 12th Mathematics Chapter 2 Important Questions and their solutions.
Also Read: Check CBSE 12th Mathematics Chapter 1 Important Questions
CBSE 12th Mathematics Chapter 2 Important Questions & Solutions
Find the CBSE 12th Mathematics Chapter 2 Important Questions and solutions for the 2nd Chapter (Inverse Trigonometric Functions) below.
- Question 1: Write the value of tan-1 (√3) – cot-1 (- √3).
Answer: We have, tan-1 (√3) – cot-1 (-√3)
= tan-1 (√3) – {π – cot-1 (√3)} [∵ cot-1 (- x) = π – cot-1 x; x ∈ R]
= tan-1 √3 – π + cot-1 √3
= (tan-1 √3 + cot-1 √3) – π
= π2 – π = – π2 [∵ tan-1x + cot-1x = π2; x ∈ R]
Which is the required principal value. - Question 2: Find the principal value of tan-1√3 – sec-1 (- 2).
Answer: We have, tan-1√3 – sec-1 (- 2)
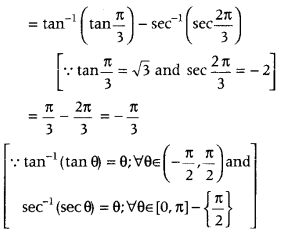
Which is the required principal value.
- Question 3: If sin (sin-115 + cos-1x) = 1, then find the value of x.
Answer: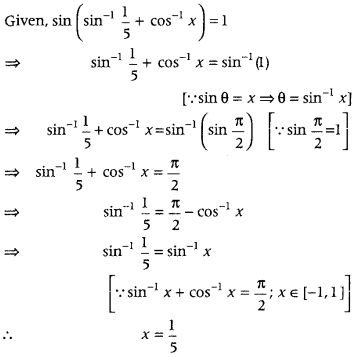
- Question 4: If tan-1x + tan-1 y = π4; xy < 1, then write the value of x + y + xy.
Answer: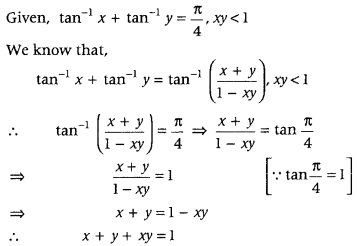
- Question 5: Write the value of cos-1(−12) + 2 sin-1(12).
Answer: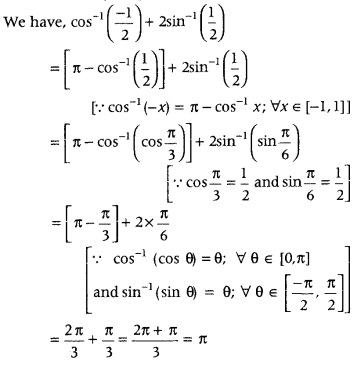
- Question 6: Write the principal value of cos-1 [cos(680)°].
Answer: First we check the given angle lies in the principal value branch. If it is so, then use the property cos1 (cos θ) = θ, ∀θ ∈ [0, 180°]. Otherwise reduce the angle such that, it lies in the principal value branch.
We know that, principal value branch of cos-1 x is [0, 180°].
Since, 680° ∉ [0, 180°], so write 680° as 2 × 360° – 40°
Now, cos-1 [cos(680)°] = cos-1 [cos(2 × 360° – 40°)]
= cos-1 (cos 4o°) [∵ cos(4π – θ) = cos θ]
Since, 40° ∈ [0, 180°]
∴ cos-1[cos(680°)] = 40° [∵ cos-1 (cos θ) = θ; ∀ θ ∈ [0, 1 80°]]
which is the required principal value. - Question 7: Write the principal value of tan-1[sin(−π2)].
Answer: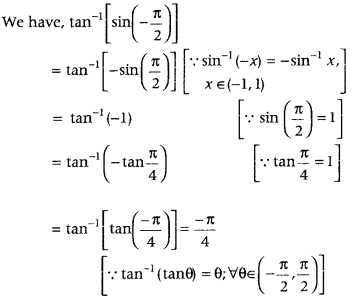
which is the required principal value. - Question 8: Find the value of the following. cot (π2 – 2 cot-1√3)
Answer: First, use cot(π2−θ) = tan θ, then put
cot-1 √3 = π6 and simplify it.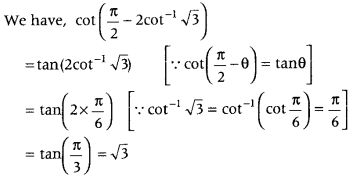
- Question 9: Write the principal value of the following. [cos−13√2+cos−1(−12)]
Answer:
- Question 10: Write the principal value of tan-1 (1) + cos-1(−12).
Answer: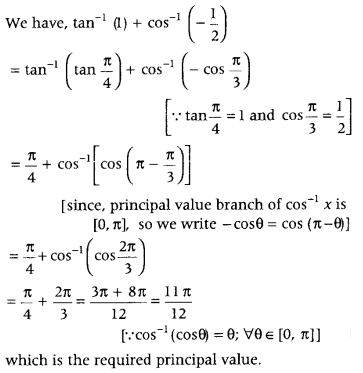
Alternate Method:
We have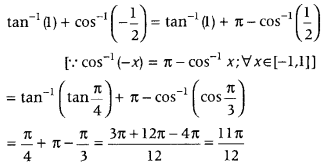
which is the required principal value. - Question 11: Write the value of tan (2 tan-115).
Answer: We have,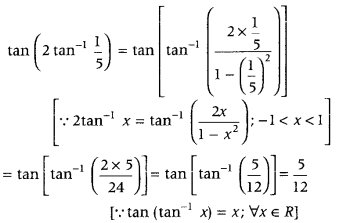
- Question 12: Write the value of tan-1[2sin(2cos−13√2)].
Answer: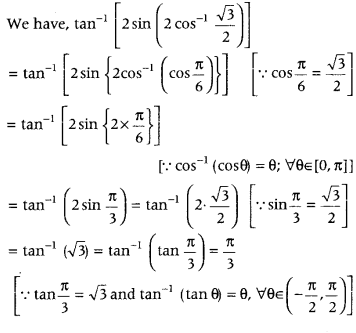
-
Question 13: Write the value of cos-1 (12) – 2 sin-1 (12).
Answer: 2π/3 - Question 14: Using the principal values, write the value of cos-1(12) + 2 sin-1(12).
Answer: 2π/3 - Question 15: Write the value of sin [π3−sin−1(−12)].
Answer:
We have,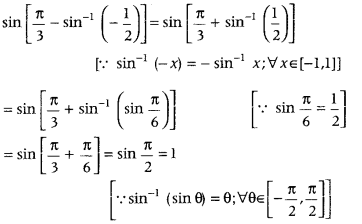
- Question 16: Write the value of tan-1(tan 3π4).
Answer: First, we check the given angle lies in the principal value branch. If it is so, then use the property tan-1 (tan θ) = θ, ∀ θ ∈ (−π2,π2), Otherwise reduce the angle such that it lies in the principal value branch.We know that the principal value branch of tan-1 x is (−π2,π2).