The area of a circle is the region occupied by the circle in a two-dimensional plane expressed by the equation A = πr2 where (Pi) π = 22/7 (or 3.14) and r is the radius of the circle.
Table of Contents
The area of a circle is defined as the space occupied by a circle in a 2-dimensional plane and is denoted by A = πr2 where (Pi) π = 22/7 (or 3.14) and r is the radius of the circle. The unit of area of a circle is the square unit, for example, m2, cm2, in2, etc.
A circle is a two-dimensional shape which does not have volume and only has an area and perimeter. The formula for the area of a circle is useful for measuring the region occupied by a circular field or a plot. This article covers details about the area of a circle, its surface area and its circumference with examples.
Definition of a Circle
A circle is a closed-plane geometric shape. It is best defined as the locus of a point moving around another fixed point at a fixed distance away from it. Basically, a circle is a closed curve with its outer line equidistant from the centre which is the radius of the circle. Some examples of a circle are a wheel, pizzas, a circular ground, etc. Let's check out a few terms used in the case of a circle.
Radius
The radius of the circle is the line that joins the centre of the circle to its outer boundary. It is generally denoted by ‘r’ or ‘R’. The radius of a circle plays an important role in the formula for the area and circumference of a circle.
Diameter
The diameter of the circle is the line that passes through its centre and equally divides it into two parts. It is two times the radius of the circle and is represented by ‘d’ or ‘D’.
Therefore,
d = 2r or D = 2R
If the diameter of the circle is known, we can calculate the radius of the circle like-
r = d/2 or R = D/2
Circumference of a Circle
The perimeter of closed figures is the total length of their outer boundaries. This perimeter is called the “circumference” of the circle which is the length of the boundary of the circle. Hypothetically, if we were to open up the circle to form a straight line, then the total length of this straight line would be the circumference.
Circumference / Perimeter = 2πr units
where ‘r’ is the radius of the circle
π is the ratio of the circumference of a circle to its diameter and is the same for every circle. Let us take a circle with a radius ‘r’ and a circumference ‘C’. For this circle:
π = Circumference/Diameter
π = C/2r
C = 2πr
What is the Area of a Circle?
Measured in square units, the area of a circle is the region covered or enclosed within its boundary. Every geometrical shape has its own area which is the region that occupies the shape in a two-dimensional plane. The total area covered by one complete cycle of the radius of the circle on a two-dimensional plane is called the area of that circle. The formula used to calculate the area of a circle is explained below.
Formula for Area of a Circle
Let us take, for example, a circle with a radius ‘r’.

In the image, the radius ‘r’ of the circle spans from the centre ‘o’ to the boundary of the circle. The area (A) of the circle is equal to the product of pi and the square of the radius which is represented as:
Area of a Circle, A = πr2 square units
Where the value of pi, π = 22/7 or 3.14 and r is the radius.
Derivation of the Area of Circle
The area of a circle can be calculated using two methods, which are:
- Determining the area of a circle using rectangles
- Determining the area of a circle using triangles
Determining the Area of a Circle Using Rectangles
In this method, the circle is divided into several small sectors and is arranged in the form of a parallelogram, as shown in the figure below. It is clear that the parallelogram can be changed into a rectangle if the circle is divided into more sectors.
As observed in the figure below, the circle is divided into 16 sectors, 8 of them are coloured blue and the rest 8 are coloured green.
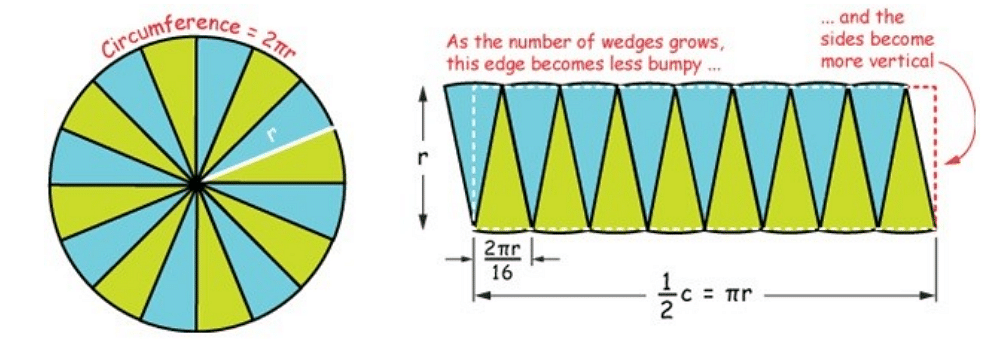
The blue and the green sectors are then arranged alternately as shown in the figure above.
Considering that the circumference of a circle is 2πr, the total length of the base of the parallelogram (rectangle as the number of sectors becomes more) will be πr (the total length of the base of the 8 blue sectors) and the height of the parallelogram (or rectangle) will be r.
So, the area of the rectangle =length×base=πr×r=πr2
We already know that the rectangle consists of the area of the sectors of the circle.
Therefore, the area of the circle is πr2.
Determining the Area of a Circle Using Triangles
In this method, the entire area of the circle is considered as consisting of several numbers of concentric circles. As shown in the figure, if the circle is cut along the radius and if all those lines (circumferences of the concentric circles) are arranged in the form of a right-angled triangle or an isosceles triangle, then a right-angled triangle or an isosceles triangle is obtained the base of which is 2πr and height is r.
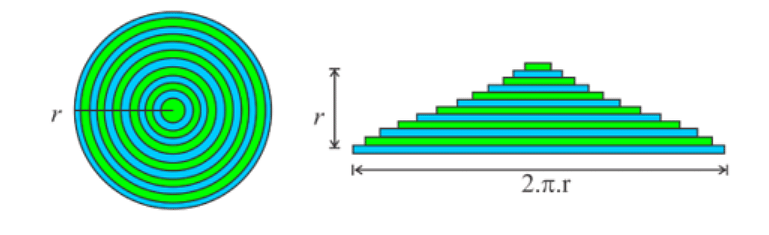
So, the area of the right-angled triangle or the area of an isosceles triangle
A =12×base×height=12×2πr×r=πr2
In this case, the area of the circle = the area of the right-angled triangle or an isosceles triangle =πr2
Surface Area of a Circle
A circle is the 2-dimensional representation of a sphere. The surface area of a circle is defined as the total area that is taken inside its boundary. The area of the circle is the same as the surface area of the circle. Sometimes, the circle’s volume also defines the area of a circle.
When the radius or diameter or even the circumference of the circle is already known, then we can use the surface formula to find out the surface area which is represented in square units.
The surface area of a circle is A = π x r2
How to Find the Area of a Circle?
We already know that the area of a circle is equal to pi times the square of its radius, i.e. πr2. To determine the area of a circle, we need to know either the radius or diameter of the circle.
For instance, if the radius of a circle is 7cm, then its area will be:
A = πr2 = π(7)2 = 22/7 x 7 x 7 = 3.14 x 49 = 154 sq.cm.
Also, if the circumference of the circle is known, we can find the area of the circle.
It is known that the circumference of a circle is 2 times of product of pi and the radius of a circle, expressed as
C = 2πr
Now we can find the value of the radius,
r = C/2π
Once, we get the value of the radius, we can easily find the area of a circle using the formula A = πr2
Difference Between the Area of a Circle and the Area of a Square
The area of a circle is estimated to be 80% of the area of a square when the diameter of the circle and the length of the side of the square is the same.
An interesting activity is to insert a circular object into a square shape with the same diameter and side length, respectively. If the area of a square is 100 sq.units, then the area of the circle will be approximately 80 sq. units of it.



















POST YOUR COMMENT