The area of parallelogram expressed as A=b*h where ‘b’ is the based and ‘h’ is the height of the parallelogram is defined as the total surface occupied by the parallelogram in a 2D space.
Table of Contents
The area of parallelogram is the region covered by a parallelogram in a two-dimensional plane. A parallelogram is a two-dimensional figure with four sides and the area of parallelogram is the space enclosed within its four sides and is equal to the product of its length and height.
A parallelogram is a special quadrilateral case, where opposite sides are equal and parallel. As it is a two-dimensional figure, it has an area and perimeter. The sum of the interior angles in a parallelogram is 360 degrees. More about the area of parallelogram along with its formula, derivations, and more solved problems are covered in this article in detail.
What is the Area of Parallelogram?
The area of parallelogram is the region it bounds in a given two-dimension space. A parallelogram is a special type of quadrilateral with a pair of parallel opposite sides. The opposite sides of a parallelogram are of equal length and the opposite angles are of equal measures.

Formula for the Area of Parallelogram
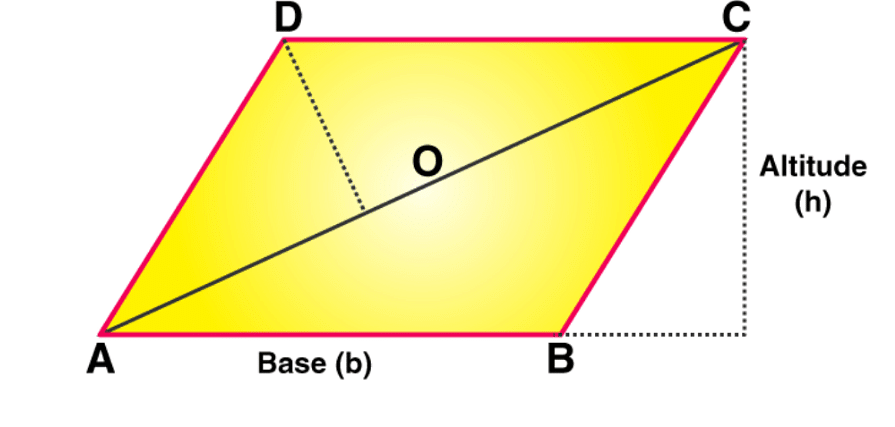
To find the area of the parallelogram, multiply its base by its height. The base and the height of the parallelogram are perpendicular to each other and the lateral side of the parallelogram is not perpendicular to the base. Therefore, a dotted line is drawn to represent the height.
Area of parallelogram = b × h square units
Where
‘b’ is the base of the parallelogram,
‘h’ is the height of the parallelogram.
How to Calculate the Area of Parallelogram?
The area of parallelogram can be calculated using its base and height. It can also be calculated if its two diagonals are known along with any of their intersecting angles or if the length of its parallel sides is known, along with any of the angles between the sides. The three methods to derive the area of parallelogram are mentioned below:
- When the base and height of a parallelogram are given
- When height is not given
- When diagonals are given
Area of Parallelogram Using Sides
Letus assume ‘a’ and ‘b’ are the set of parallel sides and ‘h’ is the height of a parallelogram, then based on the length of sides and its height, the formula for the area of parallelogram is expressed as
Area = Base × Height
A = b × h [sq.unit]
Example: If the base of a parallelogram is equal to 5 cm and the height is 3 cm, find the area of parallelogram.
Solution: It is known that the length of base=5 cm and height = 3 cm
As per the area of parallelogram formula, Area = 5 × 3 = 15 sq.cm
Area of Parallelogram Without Height
If the height of a parallelogram is not known, then we can use the concept of trigonometry to find the area of parallelogram.
Area = ab sin (x)
Where a and b are the length of adjacent sides of the parallelogram and x is the angle between its sides.
Example: The angle between any two sides of a parallelogram is 90 degrees and the length of its two adjacent sides are 3 cm and 4 cm, respectively, then find the area of parallelogram.
Solution: Let us assume that a = 3 cm and b = 4 cm
x = 90 degrees
Area = ab sin (x)
A = 3 × 4 sin (90)
A = 12 sin 90
We already know that sin 90 = 1
A = 12 × (1) = 12 sq.cm.
Note: The parallelogram is a rectangle if the angle between its sides is 90 degrees.
Area of Parallelogram Using Diagonals
The area of any given parallelogram can also be calculated using the length of its diagonals. As we know, a parallelogram has two diagonals which intersect each other at certain angles. Suppose the diagonals of a parallelogram intersect each other at an angle ‘x’, then the area of parallelogram is given by:
Area of parallelogram= ½ × d1× d2 × sin (y)
Where d1 and d2 are the lengths of diagonals of the parallelogram
‘y’ is the angle between the diagonals.

Check the table below to get summarized formulas of an area of a parallelogram.
| Using Base and Height | A = b × h |
| Using Trigonometry | A = ab sin (x) |
| Using Diagonals | A = ½ × d1 × d2 × sin (y) |
Where,
b = base of the parallelogram (AB)
h = height of the parallelogram
a = side of the parallelogram (AD)
x = any angle (∠DAB or ∠ADC) between the sides of the parallelogram
d1 = diagonal of the parallelogram (p)
d2 = diagonal of the parallelogram (q)
y = any angle (∠DOA or ∠DOC) between the intersection point of the diagonals
Note: In the above figure,
DC = AB = b
AD = BC = a
∠DAB = ∠DCB
∠ADC = ∠ABC
O is the intersecting point of the diagonals of the parallelogram
∠DOA = ∠COB
∠DOC = ∠AOB
Area of Parallelogram in Vector Form
The area of parallelogram can be determined using different formulas even when either the sides or the diagonals of the parallelogram are given in the vector form. Suppose vector ‘a’ and vector ‘b’ are the two sides of a parallelogram, such that the resulting vector is the diagonal of the parallelogram shown below.

Area of parallelogram in vector form = Mod of cross-product of vector ‘a’ and vector ‘b’

Now, we have to find the area of parallelogram with respect to its diagonals, say d1 and d2, in vector form.
























POST YOUR COMMENT