The trigonometric functions sin, cos, and tan are the main functions we consider while solving any trigonometric questions. This article discusses the sin cos tan table and ways to derive values from it.
Table of Contents
The trigonometry value is used to measure the value of the angles and sides of the right-angle triangle. The foremost focus is to solve the sin, tan, and cos values of the trigonometric problems.
The sin cos and tan formula are defined in terms of two of three sides of a right-angled triangle.
Sin Cos Tan Table
The trigonometric functions of sin, cos, and tan are the main functions we consider while solving any trigonometric questions. ‘Sin cos tan table’ consists of sin, cos, and tan values of standard angles 0°, 30°, 45°, 60°, and 90°, and sometimes other angles like 180°, 270°, and 360° also.
Provided below is a chart that can be used to determine the angles.
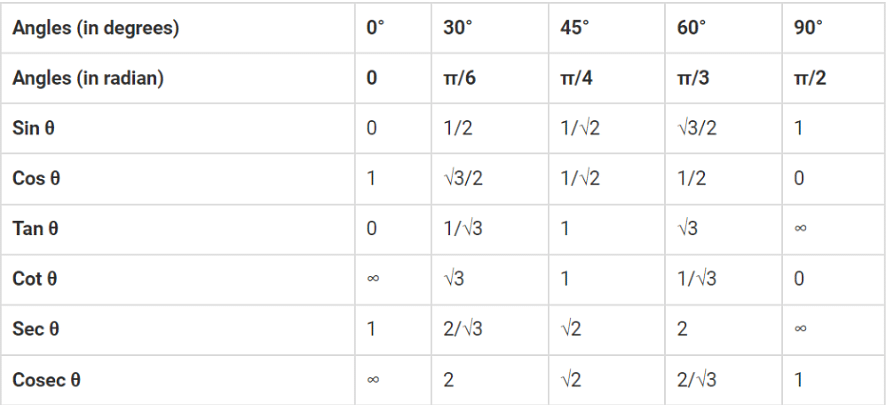
The sin cos and tan table helps to find the values of trigonometric standard angles such as 0°, 30°, 45°, 60°, and 90°. It consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant, cotangent.
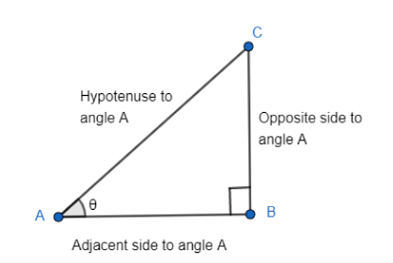
sin θ = Opposite/Hypotenuse
cos θ = Adjacent/Hypotenuse
tan θ = Opposite/Adjacent
How to Solve Sin Cos Tan Values?
The following steps will help in remembering the trigonometric values.
- Firstly divide the numbers 0,1,2,3 and 4 by 4 and then take the positive roots of all those numbers.
- We get the values for sine ratios,i.e., 0, ½, 1/√2, √3/2, and 1 for angles 0°, 30°, 45°, 60° and 90°
- Write the values of sine degrees in reverse order to get cosine values for the same angles.
- As we know, tan is the ratio of sin and cos, such as tan θ = sin θ/cos θ. Thus, we can get the values of the tan ratio for the specific angles.
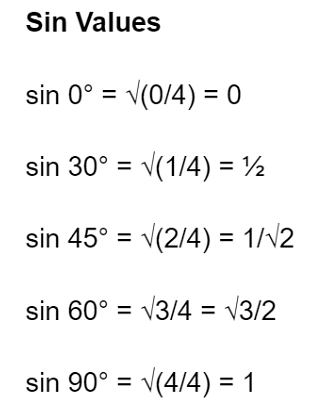
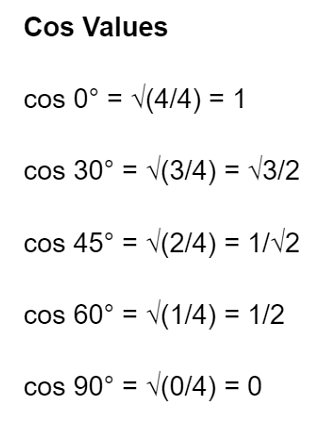

Solved Examples Using Sin Cos Tan Table Formula
The solved examples using the Sin Cos Tan table formula will help to understand the concept of the formulas given in the table discussed above. Check the solved questions given below
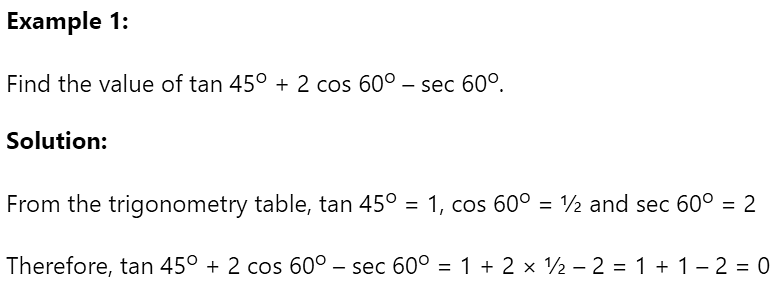
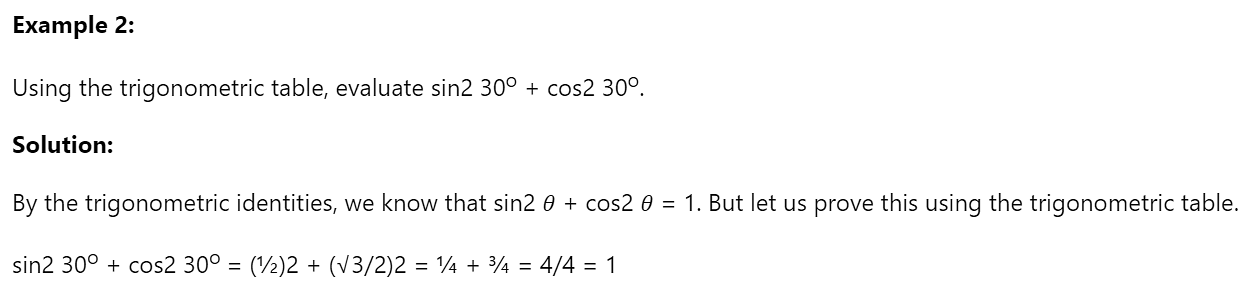
Steps to Create a Trigonometric Table
- A table with the top row listing the angles, such as 0°, 30°, 45°, 60°, and 90°, must be created with trigonometric functions in the first column, such as sin, cos, tan, cosec, sec, cot.
- Determine the value of Sin: To determine the values of sin, divide 0, 1, 2, 3, and 4 by 4 under the root, respectively.
- Determine the value of Cos: The cos-value is the opposite angle of the sin angle. To determine the value of cos, divide by 4 in the opposite sequence of sin. For example, divide 4 by 4 under the root to get the value of cos 0°.
- Determine the value of Tan: The tan is equal to sin divided by cos. Tan = sin/cos. To know the value of tan at 0°, divide the sin at 0° by the value of cos at 0°.
- Determine the value of Cot: The value of cot is equal to the reciprocal of tan. The value of the cot at 0° will be obtained by dividing 1 by the value of tan at 0°.
- Determine the value of Cosec: Cosec at 0° is the reciprocal of sin at 0°. Cosec 0°= 1/0 = Infinite or Not Defined.
Determine the value of Sec: The value of sec can be obtained by all common cos values. The sec value on 0° is the opposite of cos on 0°



















POST YOUR COMMENT