NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables: Important Questions

The NCERT solutions for class 10 Maths chapter 3 Pair of Linear Equations in Two Variables has a total weightage of 11 marks in the examination. The NCERT solutions will help the candidates to understand how the problems under these concepts are solved. This chapter will guide the students to prepare well for the class 10 CBSE exams and the other competitive exams. 

Exam experts design the NCERT solutions for class 10 Maths chapter 3, and they are based on the latest CBSE curriculum. Moreover, students will also learn the problem-solving method of the questions presented in chapter 3 of the CBSE syllabus for 2023-24. Find below for more details on the NCERT solutions for class 10 Maths. 

Table of Contents

• NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables: Important Questions 
• Class 10 Maths Pair of Linear Equations in Two Variables Mind Map
• Key Features of NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables: Important Questions 

The NCERT solutions and questions are mentioned below for the candidates. It includes all the important questions students must consider while preparing for their final exams. 

Ex 3.1 Class 10 Maths Question 1

Aftab tells his daughter, “Seven years ago, I was seven times as old as you were then. Also, three years from now, I shall be three times as old as you will be”. Isn’t this interesting? Represent this situation algebraically and graphically.

Solution:

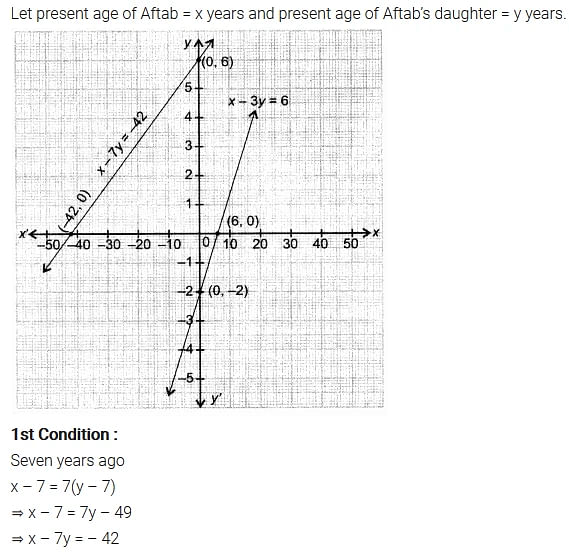
Ex 3.1 Class 10 Maths Question 2.

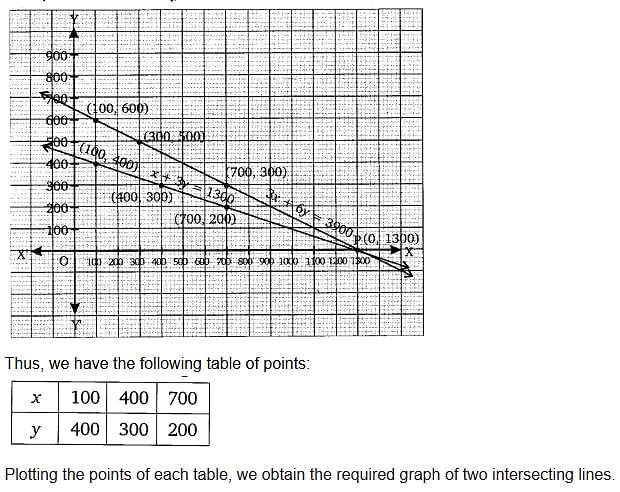
The coach of a cricket team buys 3 bats and 6 balls for ₹ 3900. Later, she buys another bat and 3 more balls of the same kind for ₹1300. Represent this situation algebraically and geometrically.

Solution:

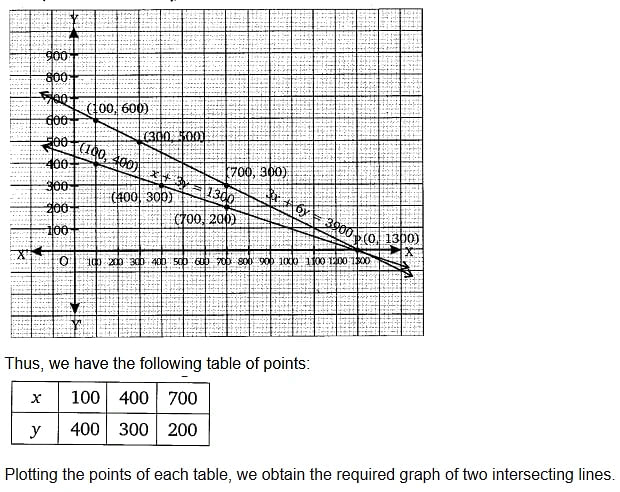
Ex 3.1 Class 10 Maths Question 3.

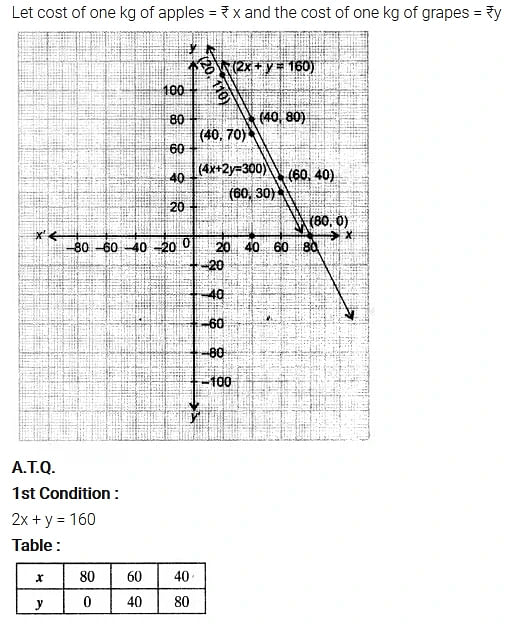
The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹160.  After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹300. Represent the situation algebraically and geometrically.

Solution:

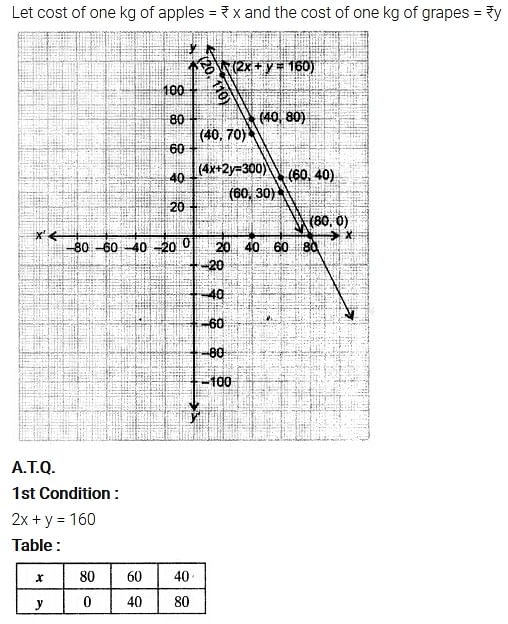
Exercise 3.2 Page: 49

Form the pair of linear equations in the following problems, and find their solutions graphically.

(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

(ii) 5 pencils and 7 pens together cost 50, whereas 7 pencils and 5 pens together cost 46. Find the cost of one pencil and that of one pen.

Solution:

(i)Let there are x number of girls and y number of boys. As per the given question, the algebraic expression can be represented as follows.

x +y = 10

x– y = 4

Now, for x+y = 10 or x = 10−y, the solutions are;

For x – y = 4 or x = 4 + y, the solutions are;

The graphical representation is as follows;

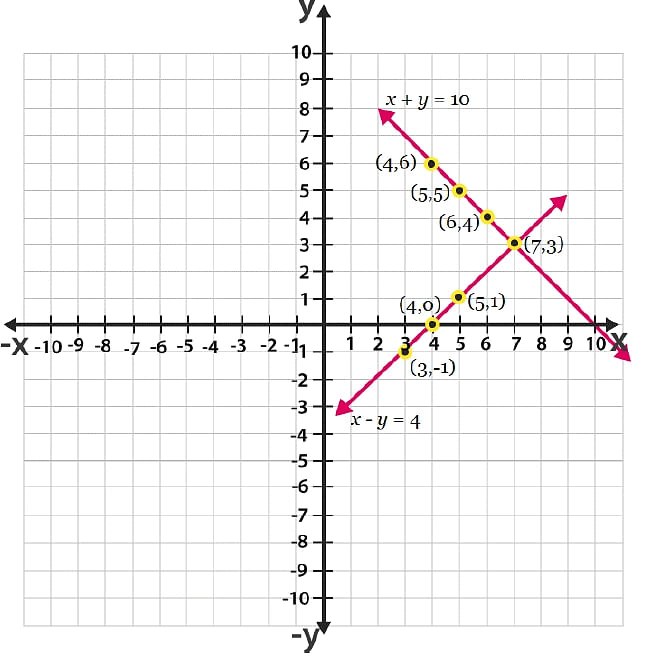
From the graph, it can be seen that the given lines cross each other at point (7, 3). Therefore, there are 7 girls and 3 boys in the class.

(ii) Let 1 pencil costs Rs.x and 1 pen costs Rs.y.

According to the question, the algebraic expression cab be represented as;

5x + 7y = 50

7x + 5y = 46

For, 5x + 7y = 50 or  x = (50-7y)/5, the solutions are;

For 7x + 5y = 46 or x = (46-5y)/7, the solutions are;

Hence, the graphical representation is as follows;

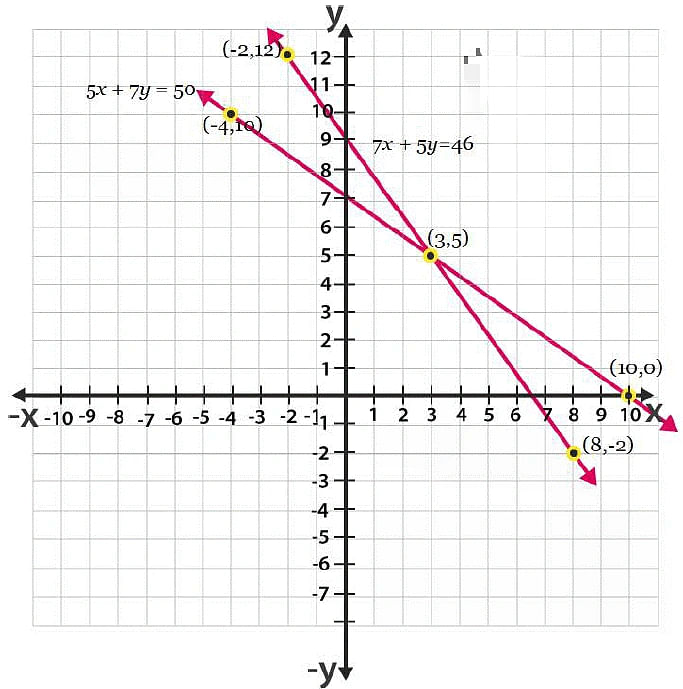
From the graph, it is can be seen that the given lines cross each other at point (3, 5).

So, the cost of a pencil is 3/- and cost of a pen is 5/-.

Ex 3.1 Class 10 Maths Question 3.

The cost of 2 kg of apples and 1 kg of grapes on a day was found to be ₹160.  After a month, the cost of 4 kg of apples and 2 kg of grapes is ₹300. Represent the situation algebraically and geometrically.

Solution:

Exercise 3.2 Page: 49

Form the pair of linear equations in the following problems, and find their solutions graphically.

(i) 10 students of Class X took part in a Mathematics quiz. If the number of girls is 4 more than the number of boys, find the number of boys and girls who took part in the quiz.

(ii) 5 pencils and 7 pens together cost 50, whereas 7 pencils and 5 pens together cost 46. Find the cost of one pencil and that of one pen.

Solution:

(i)Let there are x number of girls and y number of boys. As per the given question, the algebraic expression can be represented as follows.

x +y = 10

x– y = 4

Now, for x+y = 10 or x = 10−y, the solutions are;

For x – y = 4 or x = 4 + y, the solutions are;

The graphical representation is as follows;

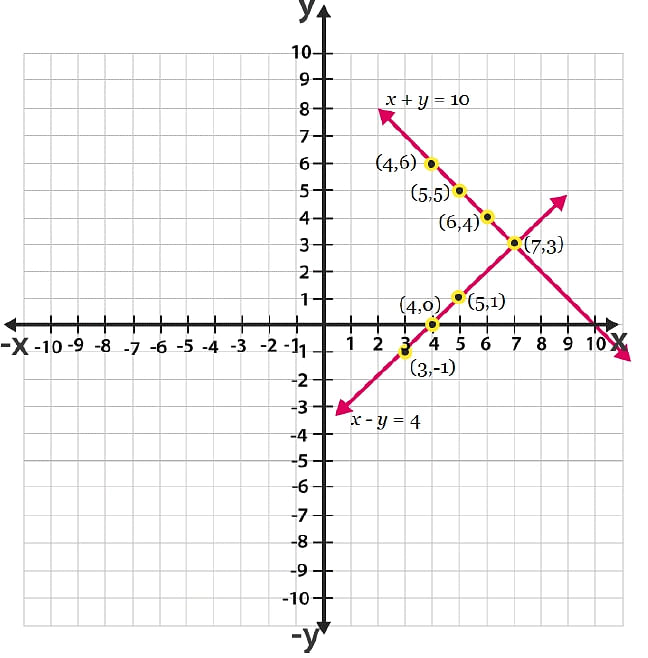
From the graph, it can be seen that the given lines cross each other at point (7, 3). Therefore, there are 7 girls and 3 boys in the class.

(ii) Let 1 pencil costs Rs.x and 1 pen costs Rs.y.

According to the question, the algebraic expression cab be represented as;

5x + 7y = 50

7x + 5y = 46

For, 5x + 7y = 50 or  x = (50-7y)/5, the solutions are;

For 7x + 5y = 46 or x = (46-5y)/7, the solutions are;

Hence, the graphical representation is as follows;

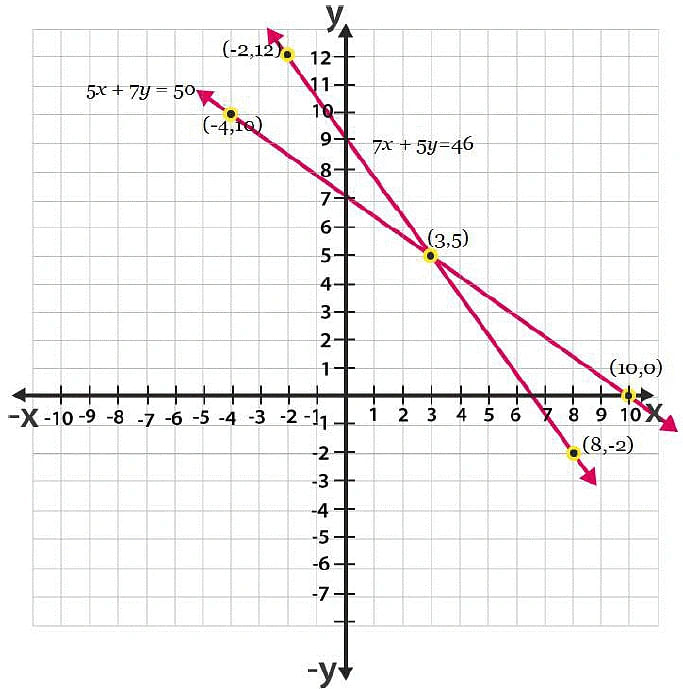
From the graph, it is can be seen that the given lines cross each other at point (3, 5).

So, the cost of a pencil is 3/- and cost of a pen is 5/-.

Class 10 Maths Pair of Linear Equations in Two Variables Mind Map

Some of the detailed topics included in the NCERT solutions for class 10 Maths chapter 3 is mentioned below for the students reference. 

System of a Pair of Linear Equations in Two Variables

An equations of the form Ax + By + C = 0 is called a linear equation in two variables x and y where A, B, C are real numbers.
Two linear equations in the same two variables are called a pair of linear equations in two variables. Standard form of linear equations in two variables.
a1x + b1y + c1 = 0, a2x + b2y + c1 = 0
where a1, a2, b1, b2, c1, c2 are real numbers such that

Representation of Linear Equation In Two Variables

Every linear equation in two variables graphically represents a line and each solution (x, y) of a linear equation in two variables, ax + by + c = 0, corresponds to a point on the line representing the equation, and vice versa.

Ploting Linear Equation in Two Variables on the Graph

There are infinitely many solutions of each linear equation. So, we choose at least any two values of one variable & get the value of other variable by substitution, i.e; Consider; Ax + By + C = 0 We can write the above linear equation as:

Here, we can choose any values of x & can find corresponding values of y.
After getting the values of (x, y) we plot them on the graph thereby getting the line representing Ax + By + C = 0.

Method of Solution of a Pair of Linear Equations in Two Variables

Coordinate of the point (x, y) which satisfy the system of pair of linear equations in two variables is the required solution. This is the point where the two lines representing the two equations intersect each other.
There are two methods of finding solution of a pair of Linear equations in two variables.
(1) Graphical Method : This method is less convenient when point representing the solution has non-integral co-ordinates.
(2) Algebraic Method : This method is more convenient when point representing the solution has non-integral co-ordinates.
This method is further divided into three methods:
(i) Substitution Method,
(ii) Elimination Method and
(iii) Cross Multiplication Method.

Algebraic Method of Solution

Consider the following system of equation
a1x + b1y + c1 =0; a2x + b2y + c1 =0
There are following three methods under Algebraic method to solve the above system.

(i) Substitution method

(a) Find the value of one variable, say y in terms of x or x in terms of y from one equation.
(b) Substitute this value in second equation to get equation in one variable and find solution.
(c) Now substitute the value/solution so obtained in step (b) in the equation got in step (a).

(ii) Elimination Method

(a) If coefficient of any one variable are not same in both the equation multiply both the equation with suitable non-zero constants to make coefficient of any one variable numerically equal.
(b) Add or subtract the equations so obtained to get equation in one variable and solve it.
(c) Now substitute the value of the variable got in the above step in either of the original equation to get value of the other variable.

(iii) Cross multiplication method

For the pair of Linear equations intwo variables:
a1x + b1y + C1 = 0
a2x + b2y + c2 = 0
Consider the following diagram.

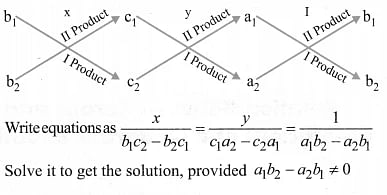
Solve it to get the solution, provided a1b2 – a2b1 ≠ 0

Equations Reducible to a Pair of Linear Equations in Two Variables

Sometimes pair of equations are not linear (or not in standard form), then they are altered so that they reduce to a pair of linear equations in standard form.
For example;

Here we substitute 

1/x = p & frac{1}{y} = q, the above equations reduces to:
a1p + b1q = c1 ; a2p – b2q = c2
Now we can use any method to solve them.

Key Features of NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables

This chapter in NCERT solution is useful for the CBSE class 10 board. The questions are designed in such a way as to improve the problem-solving abilities of the students. Some of the important features of the NCERT Solutions for Class 10 Maths Chapter 3 Pair of Linear Equations in Two Variables are mentioned below. 

• The subject experts design the NCERT solutions based on the latest CBSE syllabus 2023-24.
• Students should access chapter-wise questions and answers to boost their confidence.
• The NCERT solutions are valuable guidance for preparing students for the CBSE exams.
• The NCERT solutions are explained in a detailed procedure.