CBSE Board Exams 2023 Ongoing: Check CBSE 12th Mathematics Chapter 1 Important Questions
The CBSE will conduct the CBSE Board Exams 2023 for mathematics paper on Mar 11. This article contains some important questions from the Mathematics chapter 1.
CBSE 12th Mathematics Chapter 1 Important Questions: The Central Board of Secondary Education will conduct the CBSE Board Exams 2023 for Mathematics paper on Mar 11. The students are busy with the CBSE 12th Mathematics Revision. It will be helpful for candidates to go through the CBSE 12th Mathematics Chapter 1 Important Questions while preparing for the exam.
The Central Board of Secondary Education (CBSE) has been conducting the 12th board exams since Feb 15, 2023 and will conduct the last exam on Apr 5.
Also Read:
CBSE 12th Mathematics Important Questions
Given below is a list of CBSE 12th Mathematics Chapter 1 Important Questions from the CBSE 12th Mathematics Relations and Functions that will help the students prepare for the exam:
- Question 1: If R = {(a, a3): a is a prime number < 5} be a relation. Find the range of R.
- Answer: Given, R = {{a, cd): a is a prime number less than 5}
Since 2 and 3 are the prime numbers less than 5, a can take values 2 and 3.
Hence, R = {(2, 23), (3, 33)} = {(2, 8), (3, 27)}
Thus, the range of R is (8, 27}.
- Answer: Given, R = {{a, cd): a is a prime number less than 5}
- Question 2: Let R is the equivalence relation in the set A = {0,1, 2, 3, 4, 5} given by R = {(a, b) : 2 divides (a – b)}. Find the equivalence class [0].
- Answer: Given, R = {(a, b):2 divides(a – b)} and A = { 0,1, 2, 3, 4, 5}
Since [0] = {b ∈ A : (0, b) ∈ R}
= {b ∈ A: 2 divides (0 – b)}
= {b ∈ A : 2 divides (-b)} = {0, 2, 4}
So, equivalence class of [0] = {0,2,4}.
- Answer: Given, R = {(a, b):2 divides(a – b)} and A = { 0,1, 2, 3, 4, 5}
- Question 3: If A = {1, 2, 3}, S = {4, 5,6, 7} and f = {(1, 4), (2, 5), (3, 6)} is a function from A to B. State whether f is one-one or not.
- Answer: Given, A = {1, 2, 3} , B = {4, 5, 6, 7} and f:A → Bis defined as f = {(1, 4), (2, 5), (3, 6)}
i.e. f(1) = 4, f(2) = 5and f(3) = 6.
∴ The images of distinct elements of A under f are distinct. So, f is one-one.
- Answer: Given, A = {1, 2, 3} , B = {4, 5, 6, 7} and f:A → Bis defined as f = {(1, 4), (2, 5), (3, 6)}
- Question 4: Write fog, if f: R → R and g:R → R are given by f(x) = |x| and g(x) = |5x – 2|.
- Answer: Given, f(x) = |x|, g(x) = |5x – 2|
∴ fog (x) = f[g(x)] = f{15x – 2|}
= ||5x – 2||= |5x – 2| [∵ ||x|| = |x|]
- Answer: Given, f(x) = |x|, g(x) = |5x – 2|
- Question 5: State the reason for the relation R in the set {1, 2, 3} given by R = {(1, 2), (2,1)} not to be transitive.
- Answer: We know, for a relation to be transitive, (x, y) ∈ R and (y, z) ∈ R ⇒ (x, z) ∈ R.
Given, (1, 2) ∈ R and (2,1) ∈ R but (1,1) ∉ R.
∴ R is not transitive.
- Answer: We know, for a relation to be transitive, (x, y) ∈ R and (y, z) ∈ R ⇒ (x, z) ∈ R.
- Question 6: If f: R → R is defined by f(x) = (3 – x3)1/3, then find fof(x). (All India 2010)
- Answer: Given function is f: R → R such that f(x) = (3 – x3)1/3.
Now, fof(x) = f[f(x)] = f[(3 – x3))1/3]
= [3 – {(3 – x3)1/3}3]1/3
= [3 – (3 – x3)]1/3 = (x3)1/3 = x
- Answer: Given function is f: R → R such that f(x) = (3 – x3)1/3.
- Question 7: If f is an invertible function, defined as f(x) = 3x−45, then write f-1(x).
- Answer: Given, f(x) = 3x−45 is an invertible function.
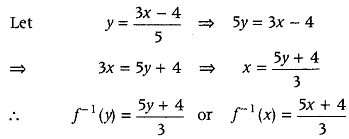
- Answer: Given, f(x) = 3x−45 is an invertible function.
- Question 8: If f(x) = 27x3 and g(x) = xy3, then find gof(x).
- Answer: Given, f(x) = 27x3 and g(x) = xy3
Now, gof(x) = g[f(x)] = g(27x3)
= (27x3)1/3 = (27)1/3.(x3)1/3
= (33)1/3 (x3)1/3 = 3x
∴ gof(x) = 3x
- Answer: Given, f(x) = 27x3 and g(x) = xy3
- Question 9: If the function f:R → R defined by f(x) = 3x – 4 is invertible, then find f-1.
- Answer: f-1 = x+43
- Answer: f-1 = x+43
- Question 10: If f,g :R → R are two functions defined as f(x) = |x| + x and g(x) = |x| – x, ∀ x ∈ R. Then, find fog and gof.
- Answer: Given, f(x) = |x| + x and g(x) = |x| – x, ∀ x ∈ R.
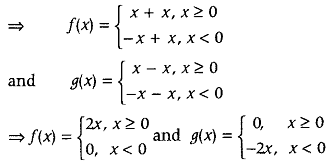
Thus, for x ≥ 0,gof (x) = g(f(x)) = g(2x) = 0
and for x < 0, gof(x) = g(f(x)) = g(0) = 0 ⇒ gof(x) = 0, ∀ x ∈ R Similarly, for x > 0, fog (x) = f(g(x)) = f(0) = 0
and for x < 0, fog (x) = f(g(x)) = f(-2x)
= 2(-2x) = -4x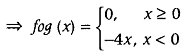
- Answer: Given, f(x) = |x| + x and g(x) = |x| – x, ∀ x ∈ R.
- Question 11: Let f: N → R be a function defined as f(x) = 4x2 + 12x + 15.Show that f:N → S, where S is the range of f, is invertible. Also, find the inverse of f.
- Answer:
f-1(x) = √(x−6)−32
- Answer:









POST YOUR COMMENT