Boyle's law: Definition, Graph, Formula, and Equation

Boyle's law, discovered by the Anglo-Irish chemist Robert Boyle in 1662 states that the pressure exerted by a gas (of a given mass, kept at a constant temperature) is inversely proportional to the volume occupied by it. This means the pressure and volume of a gas are inversely proportional to each other when the temperature and the quantity of gas are kept constant.

Boyle's law, also known as, Mariotte’s law can be derived from the kinetic theory of gases assuming a perfect (ideal) gas. Real gases comply with Boyle’s law at sufficiently low pressures, although the product pv generally decreases slightly at higher pressures, where the gas begins to depart from ideal behaviour. Mathematically, Boyle's law can be stated as P ∝ 1/V meaning pressure is inversely proportional to the volume where P is the pressure of the gas and V is the volume of the gas.

What is Boyle's Law?

Boyle's law states that the absolute pressure exerted by a given mass of an ideal gas is inversely proportional to the volume it occupies if the temperature and amount of gas remain unchanged within a closed system. When the temperature of a given mass of confined gas is constant, the product of its pressure and volume is also constant. While comparing the same substance under two different sets of conditions, Boyle's law can be expressed as:

P₁V₁=P₂V₂

which shows that as the volume increases, the pressure of a gas decreases proportionally, and vice versa. The graph below shows the hyperbolic curve of the relationship between pressure (P) and volume (V) of the form P = k/V.

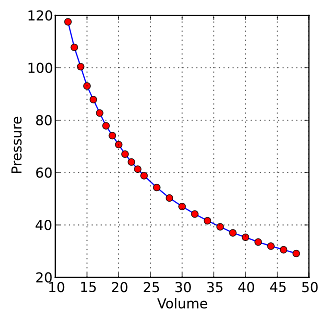
Boyle's Law Formula and Derivation

According to Boyle’s law, any change in the volume occupied by a gas (when the quantity and temperature of a gas are kept constant) will result in a change in the pressure exerted by it. In other words, the product of the initial pressure and the initial volume of a gas is equal to the product of the final pressure and final volume of a gas (which is at a constant temperature and number of moles). The mathematical expression of the same is mentioned below:

P₁V₁ = P₂V₂

Where

P₁ is the initial pressure exerted by the gas

V₁ is the initial volume occupied by the gas

P₂ is the final pressure exerted by the gas

V₂ is the final volume occupied by the gas

This expression can be derived from the pressure-volume relationship indicated by Boyle’s law. PV = k for a fixed amount of gas at a constant temperature. Therefore,

P₁V₁= k (initial pressure * initial volume)

P₂V₂= k (final pressure * final volume)

Therefore, P₁V₁ = P₂V₂

This equation predicts the increase in the pressure exerted by a gas on the walls of its container when the volume of its container is decreased (and its quantity and absolute temperature remain unchanged).

Boyle's Law Examples

Example 1- Baloon

One of the best examples to demonstrate Boyle's law in action can be seen in a balloon. Air is blown into the balloon. The pressure of that air pushes on the rubber, which makes the balloon expand. If one end of the filled balloon is squeezed, the volume occupied by the air inside the balloon decreases. Also, there is an increase in the pressure exerted by the air on the balloon, making the un-squeezed part of the balloon expand out. There is a limit to how much air/gas can be compressed. As the balloon is squeezed further, the increasing pressure eventually causes the balloon to break.

Example 2- Spray Paint

Another example demonstrating Boyle’s law is the working mechanism of spray paint. A certain amount of pressure is exerted by the paint molecules on the body of the can which holds it. When the top of the can is pressed, the volume inside the can decrease and the paint is sprayed out with great pressure. As per Boyle’s law, pressure has an inverse relationship with volume which can be observed through spray paint in action.

Solved Exercises on Boyle’s Law

Exercise 1

A particular balloon designed by a manufacturer is to be inflated to a volume of no more than 2.5 litres. If the balloon is filled with 2.0 litres of helium at sea level (101.3 kPa) and rises to an altitude at which the boiling temperature of the water is only 88℃, will the balloon burst?

Solution: There is no way of determining the starting temperature of the gas. However, we know that the boiling point of water is 100 °C at sea level. So,

Using a ratio and proportion to estimate the pressure required for water to boil at 88 °C:

100 °C is to 101.3 kPa as 88 °C is to x
x = 89.144 kPa

Now, we can try to solve the problem using Boyle's Law:

P1V1 = P2V2
(101.3) (2.0) = (88.144) (x)
x = 2.27 L
Therefore the balloon will not burst.

Exercise 2
Two bulbs of different volumes are separated by a valve. The valve between the 2.00 litre bulb, in which the gas pressure is 1.00 atm, and the 3.00 litre bulb, in which the gas pressure is 1.50 atm, is opened. What is the final pressure in the two bulbs while the temperature is kept constant and the same in both bulbs?

Solution: Using Boyle’s law to solve the problem,
P1V1 = P2V2 *2

(1.00 atm) * (2.00 L) = (x) * (5.00 L)
x = 0.400 atm

(1.50 atm) * (3.00 L) = (y) * (5.00 L)

y = 0.900 atm
Finally adding both x and y
0.400 atm + 0.900 atm = 1.30 atm

Exercise 3

An ideal gas exerts a pressure of 3 atm in a 2 L container. What will the pressure be if the volume of the container is changed to 1 L at a constant temperature?

Solution: P ∝ 1/V

=> PV=c

=> P₁V₁= P₂V₂

(3 atm) (2L) = (x) (1L)

x= (3 atm) (2L)/ (1L)

x = 6 atm

FAQs on Boyle’s Law

Q1: How does Boyle’s law work?

Ans: Boyle’s law states that the pressure (p) of a given quantity of gas is inversely proportional to its volume (v) at a constant temperature. As volume increases, the pressure falls (and vice versa) when the temperature is kept constant.

Q2: Why is Boyle's law important?

Ans: Boyle’s law explains the behaviour of gases. It proves that the pressure and volume of a gas are inversely proportional. When pressure is applied to a gas, the volume shrinks and the pressure rises.

Q3: What is the formula for Boyle’s gas law?

Ans: The empirical relation, formulated by the physicist Robert Boyle in 1662, denotes that the pressure (p) of a given quantity of gas changes inversely with its volume (v) at constant temperature; i.e. pv = k, a constant.

Q4: What is a good example of Boyle’s Law?

Ans: A balloon is one of the best examples of Boyle’s law in action. The balloon is inflated by blowing air into it. The pressure of the air pulls on the rubber that causes the balloon to expand. When one end of the balloon is compressed, the pressure inside the balloon rises which causes the un-squeezed section of the balloon to expand outward.

Q5: Can Boyle’s law be experimentally proven?

Ans: Boyle’s law explains the connection between pressure and volume. It asserts that the pressure of a specific quantity of gas is inversely proportional to its volume under constant temperature. It is possible to prove Boyle’s law empirically.

Q6: What is Boyle’s law?

Ans: Boyle’s law is a gas law published by the Anglo-Irish chemist Robert Boyle in 1662. It states that the pressure exerted by a gas is inversely proportional to the volume occupied by it at a constant mass and temperature.

Q7: What is the relationship between pressure and volume?

Ans: The pressure and volume are inversely proportional to each other under Boyle’s law.

P ∝ (1/V)

Q8: Why does volume decrease when pressure is increased?

Ans: Volume decreases with increasing pressure because the gas particles come close to each other with increasing pressure. Likewise, volume increases with decreasing pressure because the gas particles go far away from each other with decreasing pressure.

Q9: What happens to pressure if the volume is doubled?

Ans: For a fixed mass of gas at a constant temperature, pressure is inversely proportional to volume. Pressure will be halved if the volume is doubled.

Q10: Why Boyle’s law is not applicable at high pressure?

Ans: Boyle’s law applies to low pressure and not at high pressure because gases behave like an ideal gas at high pressure.