Critical Angle Formula denoted by θcric=sin-1 nr/ni is defined as the angle of incidence which provides a 90-degree angle of refraction.
Table of Contents
Critical Angle Formula is the inverse function of the sine (refraction index/incident index). It is the angle of incidence corresponding to the angle of refraction of 90° where the light ray gets completely reflected inside the medium itself. Light always bends normally as it travels from an optically denser medium to an optically rarer medium. Due to this, light is partly reflected back into the same medium and partly refracted into the second medium at the interface of the two mediums. This phenomenon of reflection of light is called Total Internal Reflection.
Critical Angle Formula
The critical Angle is the angle of incidence, which provides a 90° angle of refraction. It is an angle of incidence value and for the water-to-air limit, the critical angle is 48.6°. The critical angle is 61° for the boundary between the glass and crown water. The actual value of the critical angle completely depends on the combination of materials present on each side of the boundary.
If µd is the refractive index is the denser medium, the refractive index of air with respect to the denser medium as per Snell’s Law is given by,
μa/μd = sin i/sin r
1/ µd = sin i/sin r (As µa= 1 for air)
If,
r = 90°, i = c
sin c /sin 90°= 1/µd
Or,
sin c = 1/µd
Or,
c = sin-1(1/µd)
If the denser medium is glass,
c = sin-1(1/µg)
The Critical Angle Formula is given as
θcric=sin-1 nr/ni
Critical Angle Formula of Glass
We already know that the refractive index of glass, n1= 1.52 and the refractive index of air, n2 = 1.00
Using the Critical Angle Formula θcritical = sin-1 (n2/n1), and applying these two values as:
θcritical = sin-1 (1.00/1.52)
Therefore, the critical angle of the glass is 41.1°
Critical Angle Formula of Diamond
We already know that the refractive index of diamond, n1= 2.42 and the refractive index of air, n2 = 1.00
Using the Critical Angle Formula θcritical = sin-1 (n2/n1), and applying these two values as:
θcritical = sin-1 (1.00/1.52)
Therefore, the critical angle of a diamond is 41.1°
Critical Angle Formula of Water
We already know that the refractive index of water, n1 = 1.00 and the refractive index of air, n2= 1.33
Using the Critical Angle Formula θcritical = sin-1 (n2/n1), and applying these two values as:
θcritical = sin-1 (1.00/1.33)
Therefore, the critical angle of water is 48.75° rounded off to 49°
What is Total Internal Reflection
When light travels from a denser medium towards a rarer medium, it is partly reflected back into the same medium and partly refracted into the second medium at the interface of the two mediums. This reflection is called internal reflection.
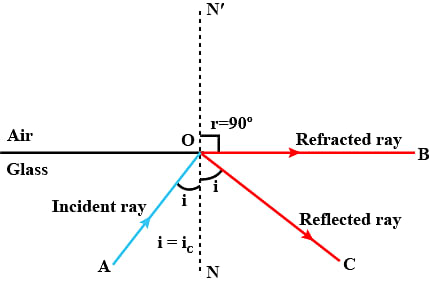
As shown in the figure above, when a ray of light (AO1B) enters from a denser medium to a rarer medium it tends to bend away from the normal. The angle of refraction (r) is greater than the angle of incidence (i) and the incident ray (AO1) is partly reflected (O1C) and partly refracted (O1B).
With the increase in the angle of incidence, the angle of refraction also increases till ray AO3, the angle of refraction for which is 90°. AO3D represents the refracted ray. If the angle of incidence is further increased (ray AO4) beyond this point, there is no occurrence of refraction and a phenomenon called total internal reflection will take place.
We must note here that the angle of incidence corresponding to the angle of refraction of 90° is called the critical angle. Mirages in a desert, the internal structure of diamonds, and optical fibres are some examples where we can see the effect of total internal reflection.
Examples of Total Internal Reflection
Some examples of total internal reflection in daily life are the formation of a mirage, the sparkling of a diamond, the transmission of light rays in an optical fibre, etc. Given below are a few real-life examples of total internal reflection.
Formation of a Mirage
A mirage is formed due to total internal reflection. During hot summers, the air present near the ground becomes much hotter than the surrounding air. The is an increase in the refractive index value of air with an increase in its density. Hotter air is less dense and has a smaller refractive index compared to cooler air.
Therefore, when the light rays travel straight through the atmosphere and move through the cold air into the hot air layer, it gets bent at the surface. A ray of light gets refracted from the normal and undergoes total internal reflection if the angle of incidence for the air near the ground is more than the critical angle.
The observer feels that light is being reflected from the ground. This optical phenomenon is called mirage which is a common occurrence in hot deserts. Another example of a mirage is the illusion of a water layer at short distances, on long straight roads during hot summers. This, in reality, is the effect of total internal reflection.
Sparkling of a Diamond
The sparkling of diamonds is caused due to total internal reflection. It is known that the refractive index of a diamond with respect to air is 2.42 and its critical angle is 24.41°. Total internal reflection takes place when light from any source makes an incidence with an angle more than its critical angle. This causes multiple internal reflections to occur as a result of which the diamond illuminates.
Transmission of Light Rays in an Optical Fibre
Optical fibres make use of total internal reflection to transmit light. Optical fibres have a solid core of dense glass surrounded by less dense cladding and are extensively used for the transmission of audio and video signals through long distances. They are covered with high-quality composite glass/quartz fibres and the refractive index of the denser core is higher than that of the rarer outer cladding.
When a light signal is directed at one end of the fibre at a certain angle, it undergoes repeated internal reflections (constantly bouncing from the cladding instead of being refracted) along the length of the optical fibre and finally emerges through its other end. There is a negligible loss in the intensity of the light signal, as it undergoes total internal reflection at each stage. Optical fibres are fabricated in such a way that the reflection of light at one side of its inner surface strikes the other side at an angle larger than the critical angle.




















POST YOUR COMMENT