Resistance Formula

The resistance Formula is denoted by the equation R=VI where R is the constant of proportionality called resistance (in ohms), V is the potential difference measured across the conductor (in volts), and I is the current passing through the conductor (in amperes). Resistance can be defined as the measure of opposition applied by any object to the flow of electric current.

The unit of electrical resistance is the ohm (abbreviated Ω), named after the German physicist and mathematician Georg Simon Ohm. The property of materials that allows the flow of electric current is known as resistance. This article covers the various electrical resistance formulas used to find the resistance offered by a conductor to the flow of current.

What is Electrical Resistance?

Resistance refers to the property of materials that allow the flow of electric current. It is a measure of the opposition to current flow in a particular electrical circuit and depends on the voltage across a specific resistor and the current flowing through it. The unit of resistance is ohms represented by the Greek uppercase letter omega Ω.

The inverse quantity of resistance refers to electrical conductance. This can be defined as the ease with which the passing of an electrical current takes place. Electrical conductance can be expressed through the equation G = 1/E, where G represents conductance and E is the voltage across the component (expressed in volts). Conductance is measured in units of siemens or mhos.

Resistance Formula

There are two methods of determining the electrical resistance of a circuit. The first one is the standard resistance formula.

R=  ρL/A

The above resistance formula represents the material's resistivity where ρ is the resistivity of the conductor, L is the length of the conductor and A is the area of the cross-section of the wire/ conductor given. This is the fundamental formula for determining the electrical resistance of any given conductor.

Calculation of Resistance Using Ohm’s Law

Ohm's law is another well-known resistance formula that is used to calculate the electrical resistance of any given system. As per Ohm's law, the current flowing through an electrical circuit is directly proportional to the voltage applied across it and inversely proportional to the resistance provided by the wire, provided the temperature remains constant. Ohm's law is expressed by the formula V= IR

Where: V is the voltage drop in the resistor (Volts, V)

I represent the current which flows through the resistor (Amperes, A)

R denotes the electrical resistance of the resistor (Ohms, Ω)

The above resistance formula can be used to calculate the electrical resistance if the values of voltage and current are known.

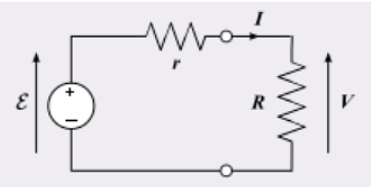
Derivation of Resistance Formula

The derivation of the resistance formula takes place from Ohm’s law which is expressed as V = IR.

When 3 resistors are connected in series, the same current flows through every resistor, but the voltage drop varies. If the applied voltage is V and the voltages across the resistances R1, R2, and R3 are V1, V2, and V3 respectively, then

V=V1+V2+V3

Ohm's law states that V = IR

Req=R1+R2+R3

Therefore, the equivalent resistance or the total resistance of the circuit can be described as a single value of resistance that can replace any number of resistors that are connected in series with no change in the value of the circuit's current or voltage.

If we have ‘n’ series resistances, the generalized formula for equivalent resistance is

Req=R1+R2+R3.......+Rn

It is already known that the applied voltage is (v)

Therefore, V=V1+V2+V3

We also know that

V = IR (from ohm’s law)

Therefore, IReq=IR1+IR2+IR1

⇒IReq=I(R1+R2+R3)⇒IReq=I(R1+R2+R3)

⇒R1+R2+R3

As a result, the equivalent resistance or the total resistance of a circuit can be defined as a single value of the resistor connected in series with changing the values of the circuit's current or voltage.

Factors Affecting Resistance

The conductor's electrical resistance is determined by the factors listed below:

• The cross-sectional area of the conductor
• The length of the conductor
• The material of the conductor and the temperature of the conducting material

Electrical resistance is directly proportional to the length of the conductor (L) and inversely proportional to the cross-sectional area (A) which is expressed through the following relation:

R = ρL/A,

where ρ is the material’s resistivity (measured in Ωm, ohm metre)

Resistivity is the qualitative measure of the ability of a material to resist flowing electric current. Popularly known as insulators, they have higher resistivity than conductors. Materials with a low resistivity value are good conductors of electricity. The values of resistivity of a few materials are mentioned below for reference:

• Silver - 1.00×10-8
• Copper - 1.68×10-8
• Aluminium - 2.82×10-8
• Wood - 1.00×1014
• Air - 2.30×1016
• Teflon - 1.00×1023

What is Resistivity?

Electric resistivity (symbolized as ρ) is defined as the electrical resistance offered per unit length and unit cross-sectional area at a specific temperature. The SI unit of electrical resistivity is Ohms.metre (Ωm). Shown below is the electrical resistivity formula:

ρ=E/J

Where

ρ is the electrical resistivity of the material expressed in Ω.m (ohm.metre)

E is the electric field in V.m-1

J is the current density in A.m-2

Difference between Resistance and Resistivity

Resistance and resistivity are two very different properties of a conductor. Resistance is the property of the conductor which opposes the flow of electric current whereas resistivity is the resistance offered by the material per unit length for a unit cross-section. More differences between resistance and resistivity are tabulated below:

Parameters	Resistance	Resistivity
Definition	Electrical resistance occurs when there is an opposition to the flow of electrons in a material.	Resistivity occurs when resistance is offered
Formula	R = V/I	ρ=E/J
SI Unit	Ohms (Ω)	Ohms.metre (Ω.m)
Symbol	R	ρ
Dependence	Depending on the length and cross-sectional area of the conductor, as well as the temperature	Temperature