The volume of hemisphere is half the volume of a sphere and is expressed as, Volume of hemisphere = 2πr3/3, where r is the radius of the hemisphere and π is a constant of value equal to 3.14 approximately.
Table of Contents
The volume of hemisphere derived by Archimedes is (2/3)πr3 cubic units where π is a constant whose value is equal to 3.14 approximately and ‘r’ is the radius of the hemisphere. A hemisphere is a 3D object which is exactly half of a full sphere, for example, bowls, headphones, Igloo, domes in architecture, etc.
The volume of hemisphere is the space occupied by the hemisphere which is half the volume of a sphere. A body with a larger volume occupies more space.
What is the Volume of Hemisphere?
A hemisphere is a 3D (three-dimensional) shape that is half of a sphere. It has a curved surface and one flat circular base. The volume of hemisphere is the total number of unit cubes that can fit into it. The unit of volume is cubic units, therefore, the volume of hemisphere can be expressed as m3, cm3, in3, etc.
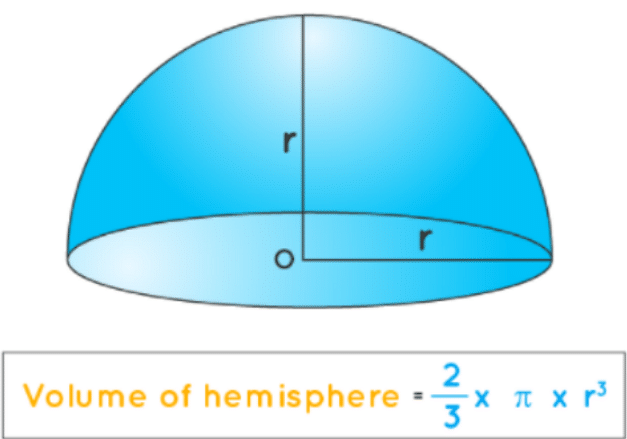
The volume of hemisphere is particularly easy to find since the base of the sphere is circular. It is expressed by the formula
Volume of hemisphere = (2/3)πr3 cubic units.
Where π is a constant of value equal to 3.14 approximately
“r” is the radius of the hemisphere
Derivation of Volume of Hemisphere
Now, let us see the derivation of the formula for the volume of hemisphere
Since a hemisphere is half of a sphere, we can divide the volume of a sphere by 2 to get the volume of hemisphere.
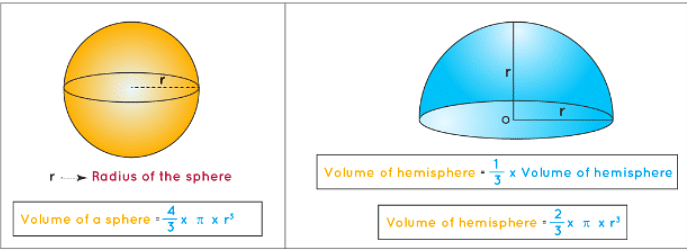
Now let us consider that the radius of a sphere is r.
The volume of the sphere can be found using the formula
Volume of Sphere = 4πr3/3
So, the volume of hemisphere = 1/2 of 4πr3/3 = 1/2 × 4πr3/3 = 2πr3/3
Definition of Hemisphere
A sphere is defined as a set of points in three-dimension where all the points lying on the surface are equidistant from the centre. When a sphere is cut across at the centre or in equal parts by a plane, it forms a hemisphere. A hemisphere is one exact half of a sphere.
In general, a sphere makes two exact hemispheres. One of the best examples of the hemisphere is the earth which consists of two hemispheres, namely the Southern Hemisphere and the Northern Hemisphere.
Hemisphere Equation
When the radius “R” is centred at the origin, the equation for the hemisphere is given by
x2 + y2 + z2 = R2
The Cartesian form/ equation of a hemisphere with the radius “R” at the point (x0, y0, z0) is given as
(x-x0)2 + (y- y0)2 + (z- z0)2 = R2
Hence, the spherical coordinates of the hemisphere are as follows
x = r cos θ sin ∅
y = r sin θ cos ∅
z = r cos ∅























POST YOUR COMMENT