The NCERT solutions for class 10 Maths chapter 1 Real Numbers is constructed by the subject experts with detailed descriptions. Solving these solutions will provide excellent practice for the students.
The NCERT solutions for class 10 Maths chapter 1 Real Numbers include topics like Fundamental Theorem of Arithmetic (H.C.F. and L.C.M.) and more. In class 10 Mathematics, two types of numbers are included in the syllabus - Real Numbers and Imaginary Numbers. Moreover, a detailed step-by-step explanation is given for each question in the NCERT solutions. These solutions are prepared by exam experts based on the latest CBSE curriculum.
In the NCERT solutions for class 10 Maths chapter 1 students are introduced to several new concepts. These new concepts will be useful for the students who wish to pursue Mathematics as a subject in class 11. Based on the NCERT solutions, students can prepare for their upcoming board exams.
Table of Contents
- Download PDF of NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers
- NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers: Important Questions
- Important Topics Under NCERT Solutions for Class 10 Maths Chapter 1
- Formula of NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers
- How to use NCERT Solutions for Class 10 Maths Chapter 1?
Download PDF of NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers
The PDF link for the NCERT solutions for real numbers class 10 is below. The pdf includes the detailed solution students must follow to prepare for the board exams. Moreover, these solutions are based on the latest exam pattern and marking scheme.
| NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers | Download |
NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers: Important Questions
Some of the important questions on the NCERT solutions for real numbers class 10 are mentioned below. The NCERT solutions for Real Numbers carry detailed explanations for every question in simple, comprehensive, and step-by-step explanations.
Exercise 1.1 Page: 7
Use Euclid’s division algorithm to find the HCF of:
- 135 and 225
- 196 and 38220
- 867 and 255
Solutions:
1. 135 and 225
As you can see from the question, 225 is greater than 135. Therefore, by Euclid’s division algorithm, we have,
225 = 135 × 1 + 90
Now, remainder 90 ≠ 0, thus again using division lemma for 90, we get,
135 = 90 × 1 + 45
Again, 45 ≠ 0, repeating the above step for 45, we get,
90 = 45 × 2 + 0
The remainder is now zero, so our method stops here. Since, in the last step, the divisor is 45, therefore, HCF (225,135) = HCF (135, 90) = HCF (90, 45) = 45.
Hence, the HCF of 225 and 135 is 45.
2. 196 and 38220
In this given question, 38220>196, therefore the by applying Euclid’s division algorithm and taking 38220 as divisor, we get,
38220 = 196 × 195 + 0
We have already got the remainder as 0 here. Therefore, HCF(196, 38220) = 196.
Hence, the HCF of 196 and 38220 is 196.
3. 867 and 255
As we know, 867 is greater than 255. Let us apply now Euclid’s division algorithm on 867, to get,
867 = 255 × 3 + 102
Remainder 102 ≠ 0, therefore taking 255 as divisor and applying the division lemma method, we get,
255 = 102 × 2 + 51
Again, 51 ≠ 0. Now 102 is the new divisor, so repeating the same step we get,
102 = 51 × 2 + 0
The remainder is now zero, so our procedure stops here. Since, in the last step, the divisor is 51, therefore, HCF (867,255) = HCF(255,102) = HCF(102,51) = 51.
Hence, the HCF of 867 and 255 is 51.
An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
Given,
Number of army contingent members = 616
Number of army band members = 32
If the two groups have to march in the same column, we have to find out the highest common factor between the two groups. HCF(616, 32), gives the maximum number of columns in which they can march.
By using Euclid’s algorithm to find their HCF, we get,
Since, 616>32, therefore,
616 = 32 × 19 + 8
Since, 8 ≠ 0, therefore, taking 32 as new divisor, we have,
32 = 8 × 4 + 0
Now we have got remainder as 0, therefore, HCF (616, 32) = 8.
Hence, the maximum number of columns in which they can march is 8.
Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let x be any positive integer and y = 3.
By Euclid’s division algorithm, then,
x = 3q+r, where q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.
Therefore, putting the value of r, we get,
x = 3q
or
x = 3q + 1
or
x = 3q + 2
Now, by taking the cube of all the three above expressions, we get,
Case (i): When r = 0, then,
x2= (3q)3 = 27q3= 9(3q3)= 9m; where m = 3q3
Case (ii): When r = 1, then,
x3 = (3q+1)3 = (3q)3 +13+3×3q×1(3q+1) = 27q3+1+27q2+9q
Taking 9 as common factor, we get,
x3 = 9(3q3+3q2+q)+1
Putting = m, we get,
Putting (3q3+3q2+q) = m, we get ,
x3 = 9m+1
Case (iii): When r = 2, then,
x3 = (3q+2)3= (3q)3+23+3×3q×2(3q+2) = 27q3+54q2+36q+8
Taking 9 as common factor, we get,
x3=9(3q3+6q2+4q)+8
Putting (3q3+6q2+4q) = m, we get ,
x3 = 9m+8
Therefore, from all the three cases explained above, it is proved that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Exercise 1.2 Page: 11
Express each number as a product of its prime factors:
(i) 140
(ii) 156
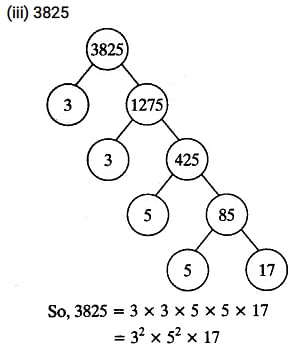
(iii) 3825
(iv) 5005
(v) 7429
Solutions:
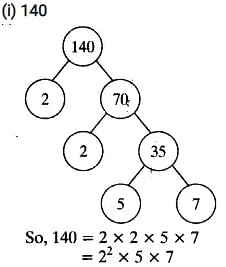
Alternatively,
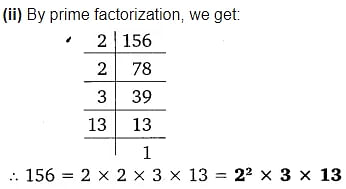
Alternatively,
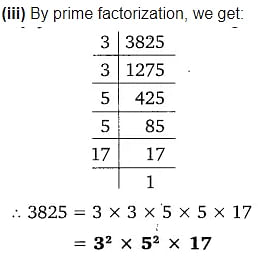
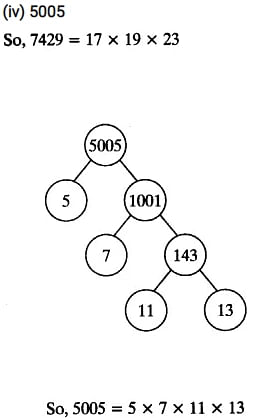
Alternatively,

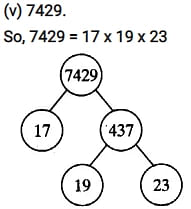
Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
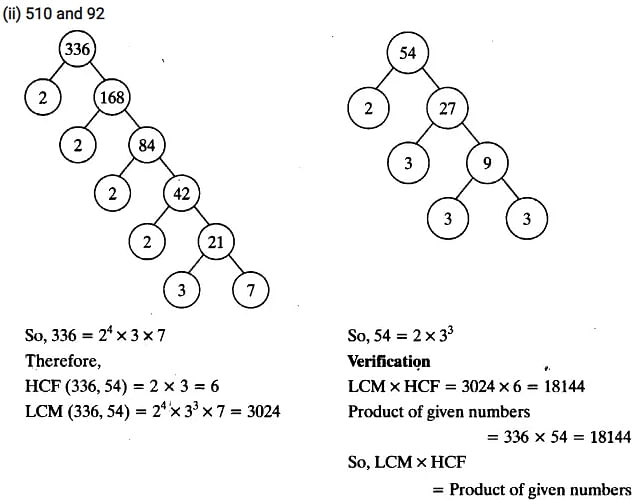
(ii) 510 and 92
(iii) 336 and 54
Solutions:
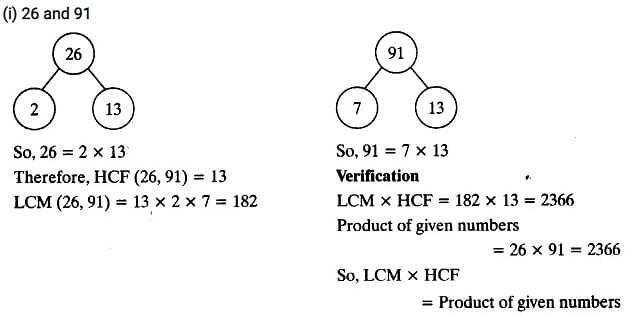
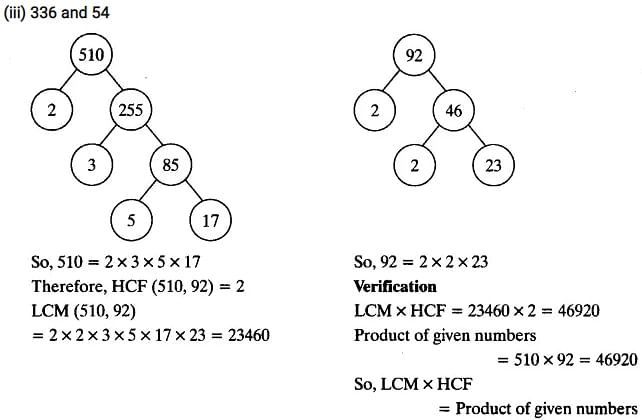
(i) 26 and 91
Given that HCF (306, 657) = 9, find LCM (306, 657).
Solution: As we know that,
HCF×LCM=Product of the two given numbers
Therefore,
9 × LCM = 306 × 657
LCM = (306×657)/9 = 22338
Hence, LCM(306,657) = 22338
There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution: Since, Both Sonia and Ravi move in the same direction and at the same time, the method to find the time when they will be meeting again at the starting point is LCM of 18 and 12.
Therefore, LCM(18,12) = 2×3×3×2×1=36
Hence, Sonia and Ravi will meet again at the starting point after 36 minutes.
Exercise 1.3 Page: 14
Prove that √5 is irrational.
Solutions: Let us assume, that √5 is rational number.
i.e. √5 = x/y (where, x and y are co-primes)
y√5= x
Squaring both the sides, we get,
(y√5)2 = x2
⇒5y2 = x2……………………………….. (1)
Thus, x2 is divisible by 5, so x is also divisible by 5.
Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we get,
5y2 = (5k)2
⇒y2 = 5k2
is divisible by 5 it means y is divisible by 5.
Clearly, x and y are not co-primes. Thus, our assumption about √5 is rational is incorrect.
Hence, √5 is an irrational number.
Prove that 3 + 2√5 + is irrational.
Solutions: Let us assume 3 + 2√5 is rational.
Then we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y
Rearranging, we get,
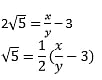
Since, x and y are integers, thus,
![]()
is a rational number.
Therefore, √5 is also a rational number. But this contradicts the fact that √5 is irrational.
So, we conclude that 3 + 2√5 is irrational.
Exercise 1.4 Page: 17
Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2352) (vii) 129/(225775) (viii) 6/15
Solutions:

Alternatively:


Alternatively:


Alternatively:






Important Topics Under NCERT Solutions for Class 10 Maths Chapter 1
Below are some important topics mentioned under the NCERT solutions for class 10 Maths chapter 1 Real Numbers. The chapter under the real numbers class 10, is divided into three parts.
| Serial Number | Topics |
| 1 | Introduction to Real Numbers |
| 2 | Fundamental Theorem of Arithmetic (H.C.F. and L.C.M.) |
| 3 | Revisiting Irrational Numbers |
Formula of NCERT Solutions for Class 10 Maths Chapter 1 Real Numbers
The following formula have been use to solve the Real Number of class 10 Maths:
- Euclid's Division Lemma states that for any positive integers a and b, there exist whole numbers q and r such that a = bq + r where 0 ≤ r < b.
- Euclid's Division Algorithm, which is based on Euclid's division lemma, outlines the procedure for finding the highest common factor (HCF) of two positive integers a and b with a > b as follows: Step 1: Apply the division lemma to find q and r where a = bq + r, 0 ≤ r < b. Step 2: If r = 0, then the HCF is b. If r ≠ 0, apply the Euclid Lemma to b and r. Step 3: Continue the process until the remainder is zero. The divisor at this stage will be the HCF (a, b). Moreover, HCF (a, b) = HCF (b, r).
- The Fundamental Theorem of Arithmetic affirms that any composite number can be represented (factorized) as a product of primes, and this factorization is unique, except for the order in which the prime factors appear.
How to use NCERT Solutions for Class 10 Maths Chapter 1?
The NCERT solutions for class 10 are very useful for the candidates as it is based on the latest CBSE class 10 syllabus pattern. Some of the important points students must consider are.
- Students must refer to the NCERT solutions for class 10 Maths as it will familiarize them with the answer structure.
- After using the NCERT solutions for class 10 Maths, students must also use the previous year's question paper to help them understand the question pattern.
- Students will score higher grades using the NCERT solutions because they contain new concepts and ideas.


POST YOUR COMMENT