The NCERT solutions for class 12 Maths chapter 2 Inverse Trigonometric Functions includes topics like properties of Inverse Trigonometric functions and basic concepts. The detailed NCERT PDF is available here.
NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions can be downloaded here in the PDF format. In the solution, every significant topic is covered with a thorough explanation to aid students in better understanding the fundamental ideas. NCERT books are essential for both board exam and competitive exam preparation.
Numerous exercises are included in Inverse Trigonometric Functions. For the student's benefit, each exercise includes answers to all of the questions as well as a step-by-step solution. Students will find this to be very useful in both their practice sessions and their homework projects. Given below are the detailed NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions.
| CBSE Class 12 Syllabus 2023-24 | CBSE Class 12 Sample Papers 2023-24 |
Table of Contents:
- NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions Download Link
- NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions Exercises
- Important Features of NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions
- Important Formulae in NCERT Solutions For Class 12 Maths Chapter 2
NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions PDF Download
The NCERT solutions for class 12 maths chapter 2 are provided in the table below for students to download. Students can click on the link and access the same.
| NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions |
NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions Exercise-wise
In NCERT Solutions for class 12 Maths chapter 2 Inverse Trigonometric Functions, inverse trigonometric functions and their characteristics will be discussed with the students. By using the offered answers, students can become familiar with the domains and ranges (primary value branches) of Inverse trigonometry class 12.
Students should keep in mind when working through difficulties on this subject that the value of an inverse trigonometric function that is located in its primary value branch is referred to as the given inverse trigonometric function's principal value. The topics explained in inverse trigonometry class 12 include:
| Exercise | Topic |
| 2.1 | Introduction |
| 2.2 | Basic Concepts |
| 2.3 | Properties of Inverse Trigonometric Functions |
| Others | Miscellaneous Q&A |
Students have previously learned about functions and the prerequisites for the inverse function's existence in prior classes. Students can discover the options for defining an inverse trigonometric function in the exercise 2.1 class 12 maths solutions. Given below are the solutions for NCERT Solutions for Class 12 Maths Chapter 2 for exercise 2.1 important questions:
Find the principal values of the following:
Question1. Find the principal value of sin-1 (-1/2)
Solution:
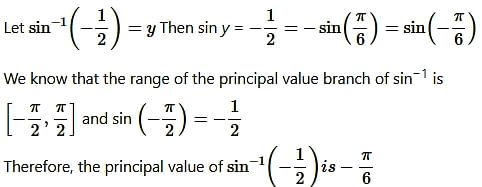
Question2. cos-1(√3/2)
Solution:
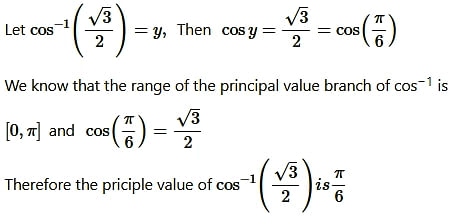
Question3. cosec-1(2)
Solution:
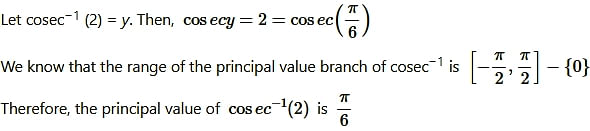
Question4. tan-1(-√3)
Solution:
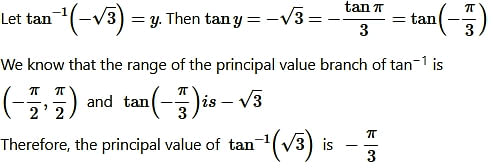
Question5. cos-1(-1/2)
Solution:
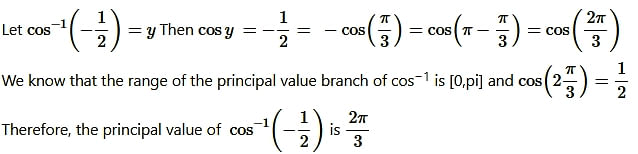
Question6. tan-1 (-1)
Solution:
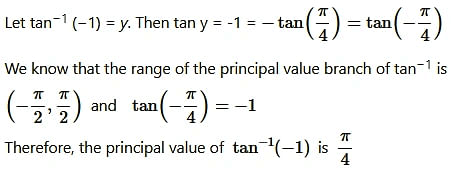
Question7. sec-1(2√3)
Solution:
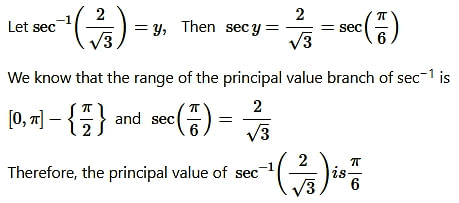
Question8. cot-1(√3)
Solution:
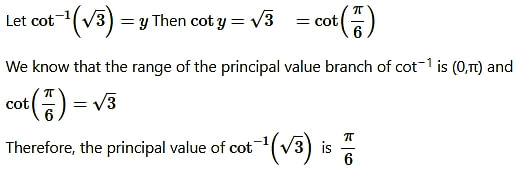
Question9. cos-1(-1/√2)
Solution:
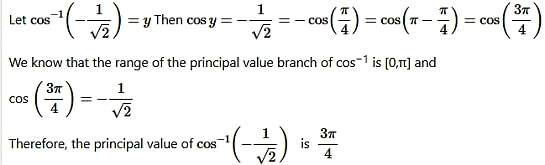
Question10. cosec-1(-√2)
Solution:

Find the value of the following:
Question11.
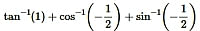
Solution:
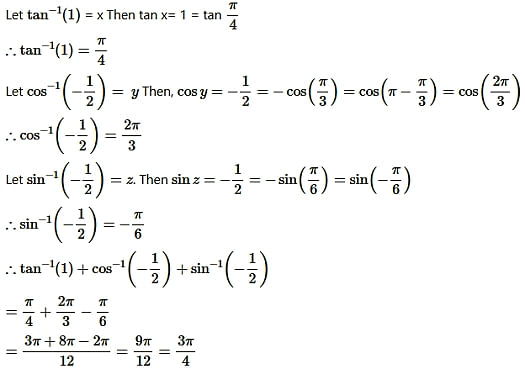
Question12.
![]()
Solution:
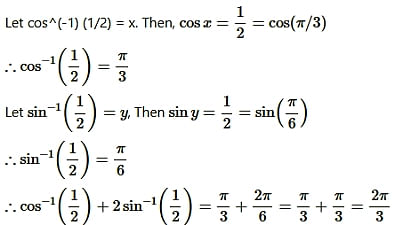
Question13.
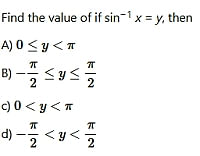
Solution:

Therefore, option (B) is correct.
Question14.

Solution:

Therefore, option (B) is correct.
Exercise 2.2 - Basic Concepts
Through NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions for exercise 2.2, students may learn about trigonometric functions including sine, cosine, tangent, cot, cosec, and sec in this exercise.
Additionally, they may learn more in-depth information on the idea of an inverse trigonometric function, including how to determine its principal value and its domain and range. In addition, inverse trigonometric function graphs are also covered. Given below is the class 12 maths chapter 2 solutions for exercise 2.2:
Prove the following:
Question1.
![]()
Solution:
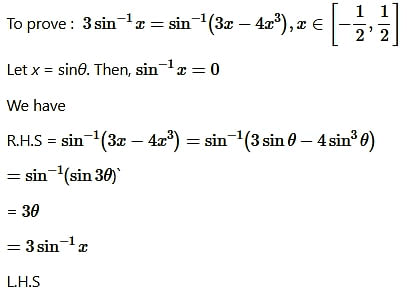
Proved.
Question2.
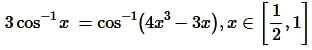
Solution:
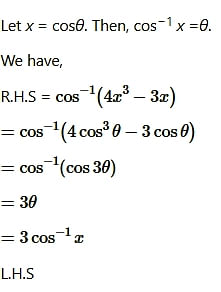
Proved.
Question3.
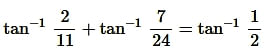
Solution:
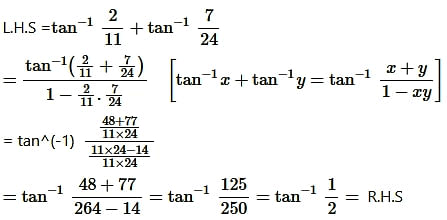
Proved.
Question 4.
![]()
Solution:
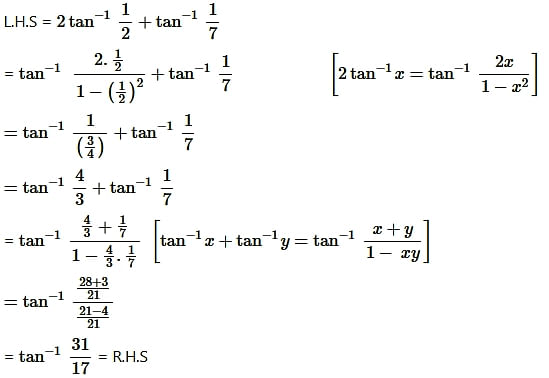
Proved.
Write the following functions in the simplest form:
Question5.
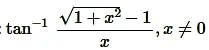
Solution:
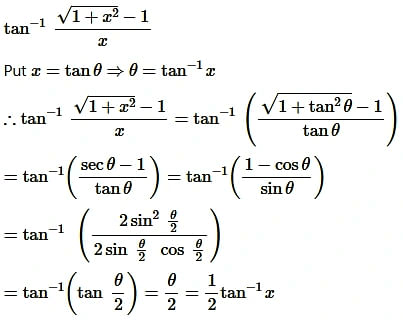
Question6.
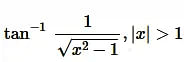
Solution:
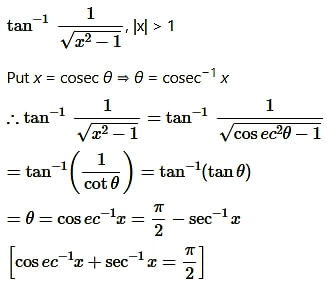
Question7.
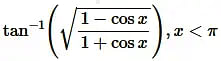
Solution:
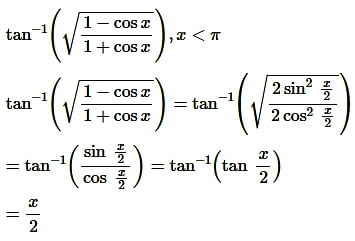
Question8.
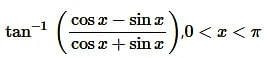
Solution:
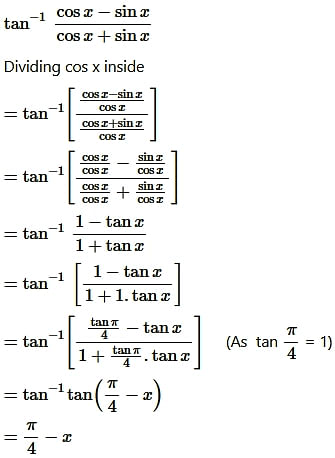
Question9.
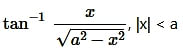
Solution:
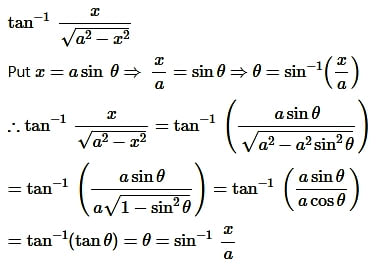
Question10.
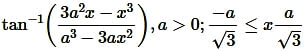
Solution:
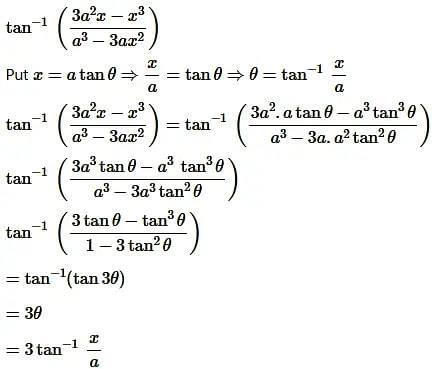
Find the values of each of the following:
Question11.
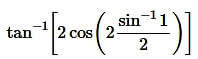
Solution:
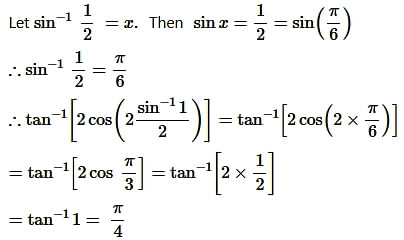
Question12.
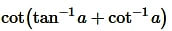
Solution:
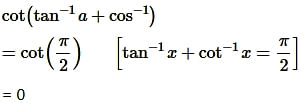
Question13.
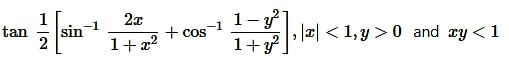
Solution:
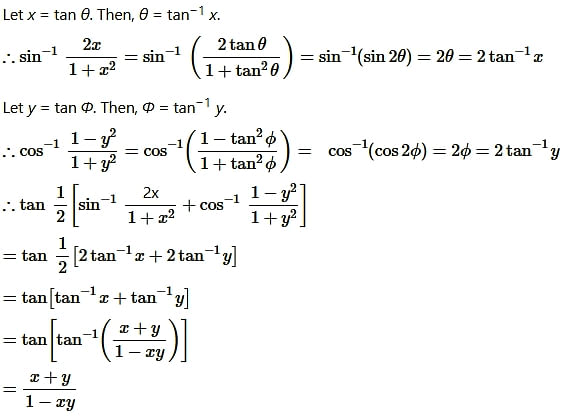
Question14. If then find the value of x
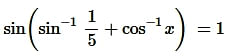
Solution:
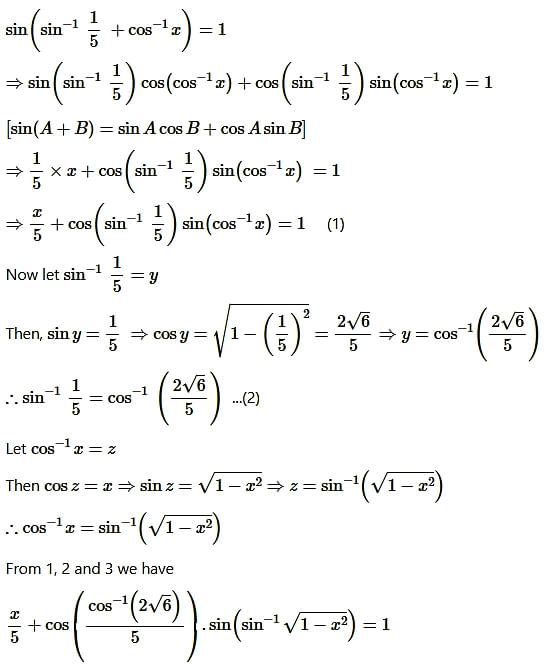
Question15. If
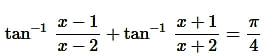
then find the value of x
Solution:
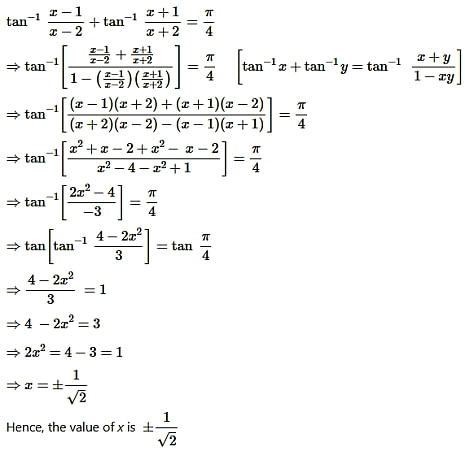
Find the values of each of the expressions in Exercises 16 to 18.
Question16.

Solution:
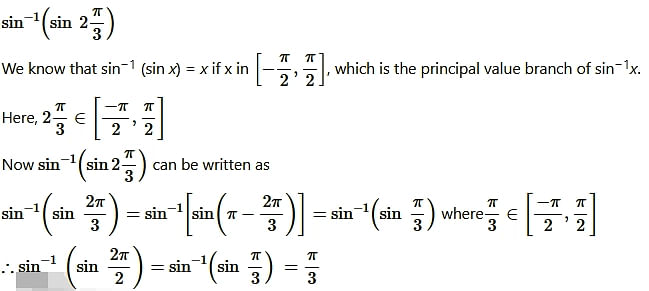
Question17.
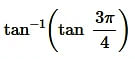
Solution:
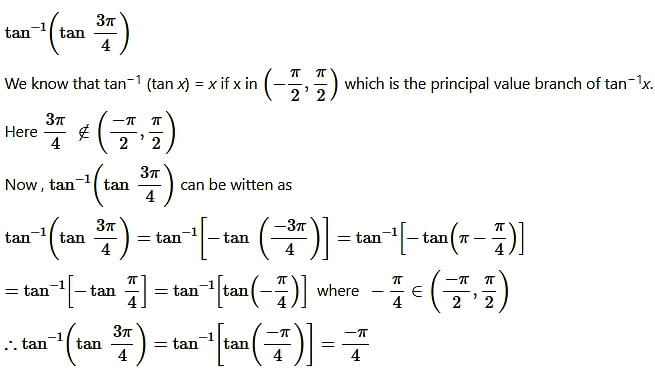
Question18.
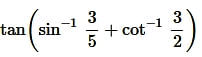
Solution:
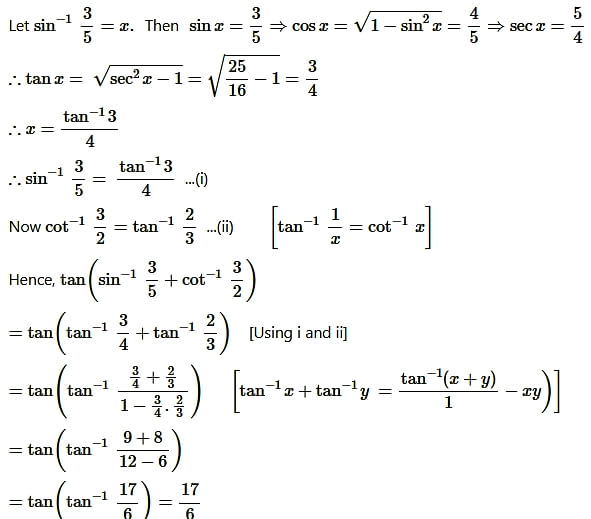
Question19.
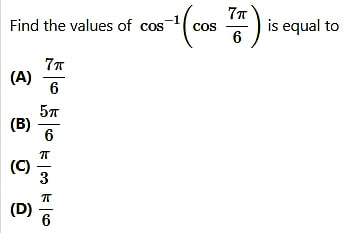
Solution:

Important Features of NCERT Solutions for Class 12 Maths Chapter 2 Inverse Trigonometric Functions
It is necessary to practise all the NCERT textbook questions of Class 12 Maths Chapter 2 to score good marks for the questions from this chapter. The NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions provided here have the following characteristics.
- The students' foundation in maths will be strengthened with the aid of NCERT solutions.
- Subject specialists carefully resolve each exercise.
- After revision, the students will be better able to understand each topic thoroughly and earn a decent grade.
- Students' confidence levels will rise as a result of these solutions.
- Since the solutions are written so that students can finish them quickly, it provides them the opportunity to work hard and get higher marks.
Important Formulae in NCERT Solutions Class 12 Maths Chapter 2
Students must utilise their critical thinking abilities while using the wide range of formulae provided in NCERT Solutions For Class 12 Maths Chapter 2 Inverse Trigonometric Functions. It is advised that they review the trigonometric formulae covered in earlier sessions because doing so will make it simpler for them to move into the main topic.
- sin–1 (–x) = – sin–1 x
- tan–1 x + cot–1 x = π/2
- sin–1 x + cos–1 x = π/2
- cos–1 (–x) = π – cos–1 x
- cot–1 (–x) = π – cot–1 x



POST YOUR COMMENT