Sin, Cos, Tan values are the basic trigonometric ratios to study the relation between angles & sides of a triangle. Learn formulae and values with easy examples.
Table of Contents
Sin, Cos, and Tan are the basic trigonometric functions considered while solving trigonometric problems. Sin, Cos, and Tan are abbreviated for sine, cosine, and tangent, respectively. These mathematical functions are used to study the relationship between the angles and sides of a triangle.
What is Sin, Cos, and Tan in Trigonometry?
While Pythagoras established the connection between the sides of a right triangle through the Pythagoras theorem, Hipparcus structured the connection between the sides and points of a right triangle utilizing the ideas of trigonometry.
However, sin, cos, and tan are essential trigonometrical proportions. Every one of which gives the proportion of different sides of a right-angled triangle. The longest side of the triangle is called ‘hypotenuse’, and the two other sides are called adjacent and opposite sides.
Sin, Cos, and Tan: Formula
Sin, cos, and tan have their formula. For example, the diagram below shows a right-angled triangle. The longest side is the hypotenuse, and the other sides are adjacent and opposite.
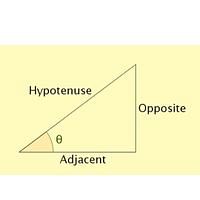 The formulas for sin, cos, and tan are as follows:
The formulas for sin, cos, and tan are as follows:
- Sine θ = Opposite side/ Hypotenuse
- Cos θ = Adjacent side/ Hypotenuse
- Tan θ = Opposite side/ Adjacent side
Therefore, we have established a relationship between sin, cos, and tan θ through the above formulas - Tan θ = Sin θ/Cos θ
Other Trigonometric Formulas
Since we have established the relationship between sin, cos, and tan, here are the other formulas:
- Tan θ = Sin θ/Cos θ
- Cot θ = Cos θ/Sin θ
- Sin θ = Tan θ/Sec θ
- Cos θ = Sin θ/Tan θ
- Sec θ = Tan θ/Sin θ
- Cosec θ = Sec θ/Tan θ
Sin θ, Cos θ, and Tan θ Value Table
The table below depicts the trigonometric functions concerning their degrees. The degrees are 0°, 30°, 45°, 60°, and 90°.
| Angles (in degrees) | 0° | 30° | 45° | 60° | 90° |
| Angles (in radian) | 0 | π/6 | π/4 | π/3 | π/2 |
| Sin θ | 0 | 1/2 | 1/√2 | √3/2 | 1 |
| Cos θ | 1 | √3/2 | 1/√2 | 1/2 | 0 |
| Tan θ | 0 | 1/√3 | 1 | √3 | Not Defined |
| Cot θ | Not Defined | √3 | 1 | 1/√3 | 0 |
| Sec θ | 1 | 2/√3 | √2 | 2 | Not Defined |
| Cosec θ | Not Defined | 2 | √2 | 2/√3 | 1 |
How to Find Sin θ, Cos θ, and Tan θ Values?
At times finding the values of the trigonometric functions can be difficult. Hence, here are some of the simple steps:
- Firstly, we can divide the numbers 0,1,2,3, and 4 by 4 and then take the positive roots of all those numbers.
- Next, we can find the sin values, i.e., 0, ½, 1/√2, √3/2, 1, with respect to their angles.
- Afterward, write the same values in reverse format to derive the cos values at 0°, 30°, 45°, 60°, and 90°.
- Further, the tan is the ratio of sin and cos. Thus, we can get the values of the tan ratio for the specific angles.
| Sin Values | Cos Values | Tan Values |
| Sin 0° = √(0/4) = 0 | Cos 0° = √(4/4) = 1 | tan 0° = 0/1 = 0 |
| Sin 30° = √(1/4) = ½ | Cos 30° = √(3/4) = √3/2 | Tan 30° = (1/2) / (√3/2) = 1/√3 |
| Sin 45° = √(2/4) = 1/√2 | Cos 45° = √(2/4) = 1/√2 | Tan 45° = (1/√2) / (1/√2) = 1 |
| Sin 60° = √3/4 = √3/2 | Cos 60° = √(1/4) = 1/2 | Tan 60° = [(√3/2)/(½)] = √3 |
| Sin 90° = √(4/4) = 1 | Cos 90° = √(0/4) = 0 | Tan 90° = 1/0 = Not Defined |
Tips to Memorize Sin θ, Cos θ, and Tan θ Value Table
Here are some of the tips that could help remember the Sin θ, Cos θ, and Tan θ value table:
- Firstly, the angles are always at 0°, 30°, 45°, 60°, and 90°.
- Next, the sin θ table goes like 0, ½, 1/√2, √3/2, 1. The immediate next table, cos θ, is just like sin θ in reverse format - likewise the rest of the table.
- Each value in the row of tan is obtained by dividing the corresponding values of sin by cos because of tan = sin/cos.
Practical Usage of Sin θ, Cos θ, and Tan θ Value
Sin, cos, and tan carry high value in solving numerous actual-life difficulties. Some of the idealistic usages of the functions are as mentioned below:
- It is employed to figure out the planetary movements.
- The functions are adopted to measure the angle of elevation, slope and heights of buildings and mountains.
- Next, the functions are of practical importance to gauge the archeological department's excavation work.
- Additionally, it is used in flight engineering to measure the angle change due to wind.
- It is also used in marine engineering.
- Moreover, it is used in civil engineering to determine the floors, loads, slopes of the roofs.
Points to Remember
As mentioned earlier, sin, cos, and tan are the basic trigonometric functions used to calculate the sides of a right-angled triangle.
- Sin θ is given by the ratio of the opposite side to the hypotenuse.
- Sin θ= Opposite/Hypotenuse = Tan θ/Sec θ
- Cos is given by the ratio of the adjacent side to the hypotenuse.
- Cos θ = Adjacent/Hypotenuse = Sin θ/Tan θ
- Tan θ is given by the ratio of sin θ to cos θ.
- Tan θ = Sin θ/Cos θ = Opposite / Adjacent.
Sample Questions
1. A ladder leans against a brick wall making an angle of 50° with the horizontal. If the ladder is at a distance of 10 ft from the wall, then up to what height of the wall the ladder reaches?
Answer:
Let us assume that the ladder reaches till x ft of the wall.
Using the given information:
Here, we know the adjacent side (which is 10 ft) and we have to find the opposite side (which is x ft). So we use the relation between the opposite and the adjacent sides which is tan.
Tan 50° = x/10
x = 10 Tan 50°
x ≈ 11.9 ft
Here, tan 50° is calculated using the calculator and the final answer is rounded up to 1 decimal. Therefore, the ladder reaches up to 11.9 ft of the wall.
2. A circus artist is climbing a 20 m long rope, which is tightly stretched and tied from the top of a vertical pole to the ground. Find the height of the pole, if the angle made by the rope with the ground level is 30°.
Answer:
Length of the rope (AC) = 20m and ∠ACB = 30º
Let the height AB of the pole be h m.
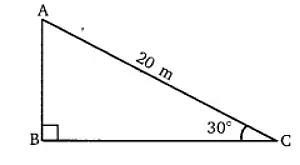
Length of the rope (AC) = 20m and ACB = 30º
Then in triangle ABC,
Sin 30 = AB/AC
½ = h/20
h = 20/2 = 10m
Hence, the height of the pole is 10 m.
3. If tan θ + cot θ = 5, find the value of tan2θ + cotθ.
Answer:
Tan θ + Cot θ = 5
Tan 2θ + Cot 2θ + 2 Tan θ Cot θ = 25 … (Squaring both sides)
Tan 2θ + Cot 2θ + 2 = 25
Therefore, Tan 2θ + Cot 2θ = 23
4.In a right triangle ABC with angle A equal to 90°, find angle B and C so that sin(B) = cos(B)
Answer:
Let b be the length of the side opposite angle B and c be the length of the side opposite angle C and h, the length of the hypotenuse.
Sin(B) = b/h and Cos(B) = c/h
Sin(B) = Cos(B) means b/h = c/h which gives c = b
The two sides are equal in length means that the triangle is isosceles and angles B and C are equal in size of 45°.
5. Simplify the trigonometric expression: 2 cot (A)-2/1 - tan(-A)
Answer:
2 Cot A-2/1 - Tan A
= (2 Cos A/Sin A)-2/1-(Sin A/Cos A)
= 2(Cos A- Sin A)/Sin A/(Cos A-Sin A)/Cos A
= 2 (Cos A-Sin A)/Sin A × Cos A/(Cos A-Sin A)
= 2 × Cos A/Sin A
= 2 × Cot A {Cot A=Cos A/Sin A}
= 2 Cot A
6. Solve the given expression using sin cos tan values: tan 60o(sec 60o/cosec 60o)
Answer:
We know, Sec 60°/Cosec 60° = Sin 60°/Cos 60°
⇒ Tan 60°(sec 60°/Cosec 60°) = Tan 60°(Sin 60°/Cos 60°) = Tan 60° × Tan 60°
⇒ (√3)2 = 3
7. Find the exact length of the shadow cast by a 15 ft lamppost when the angle of elevation of the sun is 60º.
Answer:
Let us assume that the length of the shadow of the lamp post is x ft.
Using the given information:
Applying tan to the given triangle
Tan 60° = 15/x
x = 15/Tan 60°
x = 15/√3 (Using trigonometry chart)
x = 15√3/3
Therefore, the length of the shadow of the lamp post is 15√3/3 ft.
8. If sin θ = 2/3 and tan θ < 0, what is the value of cos θ?
Answer:
It is given that sin θ is positive and tan θ is negative. So θ must be in Quadrant II, where cos θ is negative. Now, sin θ = 2/3 = Opposite/Hypotenuse.
So we can assume that Opposite = 2k, Hypotenuse = 3k.
By Pythagoras theorem,
Adjacent2 = Hypotenuse2 - Opposite2
⇒ (3k)2 - (2k)2 = 5k2
Adjacent = √5k
Therefore, Cos θ = - Adjacent/Hypotenuse = -√5k/3k = -√5/3


















POST YOUR COMMENT