The Trigonometry Formulas for JEE Main 2025 can be kept in a PDF format to aid in the last-moment revision before the exam. Trigonometry carries a weightage of 6.6% in the JEE Main Mathematics question paper.
Table of Contents
A list of Trigonometry Formulas for JEE Main 2025 is handy during the last-minute revision before the exam. Trigonometry is an important chapter in the JEE Main Mathematics syllabus and carries a weightage of 3.3%.
Trigonometry Formulas for JEE Main 2025: PDF
Trigonometry constitutes an important part of the Mathematics syllabus in the JEE Main 2025 examination. Trigonometry deals with triangles and the relationship between the sides of a triangle and its angles. Shared below is a PDF containing all the formulas in Trigonometry and are crucial for the JEE Main examination:
| Trigonometry Formulas for JEE Main | Download PDF |
Also Check: JEE Main 2025 Important Formulas
Chapter Wise Trigonometry Formulas for JEE Main 2025
The most important formulas of trigonometry have been shared below:
- sin θ = Opposite Side / Hypotenuse
- cos θ = Adjacent Side / Hypotenuse
- tan θ = Opposite Side / Adjacent Side
- sec θ = Hypotenuse / Adjacent Side
- cosec θ = Hypotenuse / Opposite Side
- cot θ = Adjacent Side / Opposite Side
- cosec θ = 1/sin θ
- sec θ = 1/cos θ
- cot θ = 1/tan θ
- sin θ = 1/cosec θ
- cos θ = 1/sec θ
- tan θ = 1/cot θ
- sin (π/2 – A) = cos A
- cos (π/2 – A) = sin A
- sin (π/2 + A) = cos A
- cos (π/2 + A) = – sin A
- sin (3π/2 – A) = – cos A
- cos (3π/2 – A) = – sin A
- sin (3π/2 + A) = – cos A
- cos (3π/2 + A) = sin A
- sin (π – A) = sin A
- cos (π – A) = – cos A
- sin (π + A) = – sin A
- cos (π + A) = – cos A
- sin (2π – A) = – sin A
- cos (2π – A) = cos A
- sin (2π + A) = sin A
- cos (2π + A) = cos A
- sin(90°−x) = cos x
- cos(90°−x) = sin x
- tan(90°−x) = cot x
- cot(90°−x) = tan x
- sec(90°−x) = cosec x
- cosec(90°−x) = sec x
- sin(x + y) = sin(x)cos(y) + cos(x)sin(y)
- cos(x + y) = cos(x)cos(y) – sin(x)sin(y)
- sin(x – y) = sin(x)cos(y) – cos(x)sin(y)
- cos(x – y) = cos(x)cos(y) + sin(x)sin(y)
- tan(x + y) = (tan x + tan y) / {1 – (tanx.tany)}
- tan(x - y) = (tan x - tan y) / {1 + (tanx.tany)}
- cos(2x) = 2cos2(x)−1 = 1–2sin2(x)
- sin (2x) = 2sin(x).cos(x) = 2 tan(x)/(1 + tan2x)
- cos (2x) = cos2x – sin2x = (1 - tan2x)/(1 + tan2x)
- tan (2x) = 2tan(x)/(1 - tan2x)
- sec (2x) = sec2x / (2 - sec2x )
- cosec (2x) = sec(x).cosec(x) / 2
- Sin 3x = 3sin(x) – 4sin3x
- Cos 3x = 4cos3x-3cos(x)
- tan (3x) = {3tan(x) – tan3x}/(1 – 3tan2x)
- sin-1 (–x) = – sin-1 x
- cos-1 (–x) = π – cos-1 x
- tan-1 (–x) = – tan-1 x
- cosec-1 (–x) = – cosec-1 x
- sec-1 (–x) = π – sec-1 x
- cot-1 (–x) = π – cot-1 x
- Sin(x).cos(y) = {sin(x+y) + sin(x-y)} / 2
- Cos(x).cos(y) = {cos(x+y) + cos(x-y)} / 2
- Sin(x).sin(y) = {cos(x-y) - cos(x+y)} / 2
- Sin(x) + sin(y) = 2 sin {(x+y)/2} cos{(x-y)/2}
- Sin(x) - sin(y) = 2 cos {(x+y)/2} sin{(x-y)/2}
- cos(x) + cos(y) = 2 cos {(x+y)/2} cos{(x-y)/2}
- cos(x) - cos(y) = -2 sin {(x+y)/2} sin{(x-y)/2}
- Sin (x/2) = ± √{(1-cos x) / 2}
- Cos (x/2) = ± √{(1+cos x) / 2}
- tan (x/2) = √{(1-cos x)/(1+cos x)} = (1 – cos x)/sin(x)
Also Read: JEE Main Maths Important Formulas 2025 - Download PDF
Basic Trigonometric Table
It is crucial to remember the trigonometric values both in terms of radian and in degrees. The most common formulas based on angles in trigonometry have been provided in the table below:
|
Angles (Radian) |
0 |
π/6 |
π/4 |
π/3 |
π/2 |
π |
3π/2 |
2π |
|
Angles (Degrees) |
0 |
30 |
45 |
60 |
90 |
180 |
270 |
360 |
|
sin |
0 |
1/2 |
1/2 |
3/2 |
1 |
0 |
-1 |
0 |
|
cos |
1 |
3/2 |
1/2 |
1/2 |
0 |
-1 |
0 |
1 |
|
tan |
0 |
1/3 |
1 |
3 |
∞ |
0 |
∞ |
0 |
|
sec |
∞ |
3 |
1 |
1/ 3 |
0 |
∞ |
0 |
∞ |
|
cosec |
∞ |
2 |
2 |
3/2 |
1 |
∞ |
-1 |
∞ |
|
cot |
1 |
2/3 |
2 |
1/2 |
∞ |
-1 |
∞ |
1 |
Also Check: JEE Main Chemistry Important Formulas 2025 - Download PDF
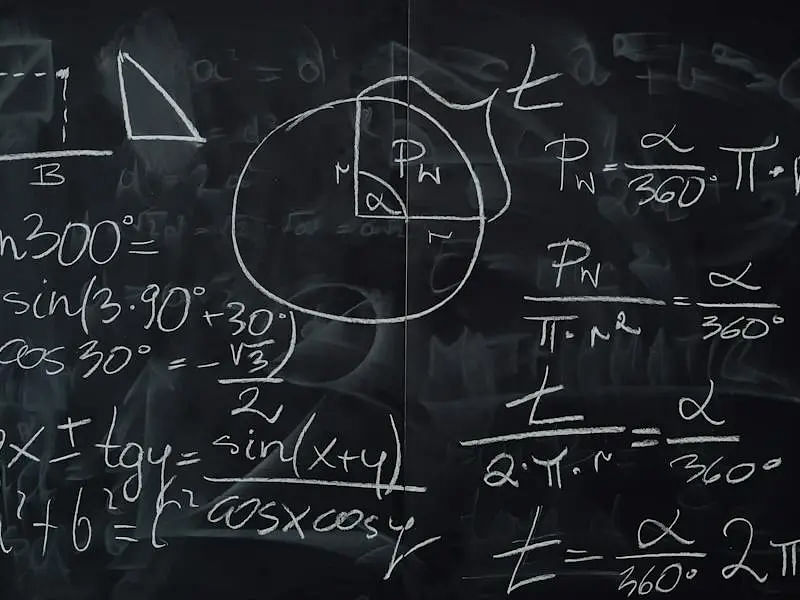





![Indian Institute of Technology, [IIT] Kanpur](https://media.getmyuni.com/azure/college-image/small/indian-institute-of-technology-iit-kanpur.jpg)
![Indian Institute of Technology, [IIT] Roorkee](https://media.getmyuni.com/azure/college-image/small/indian-institute-of-technology-iit-roorkee.jpg)
![Jawaharlal Nehru University, [JNU] New Delhi](https://media.getmyuni.com/azure/college-image/small/jawaharlal-nehru-university-jnu-new-delhi.jpg)
![University of Calcutta, [UC] Kolkata](https://media.getmyuni.com/azure/college-image/small/university-of-calcutta-uc-kolkata.jpg)

































POST YOUR COMMENT